题目内容
【题目】如图,点B、D、E在一条直线上,BE与AC相交于点F,且![]()
⑴求证:△ABC∽△ADE;
⑵求证:∠BAD=∠CAE;
⑶若∠BAD=18°,求∠EBC的度数.
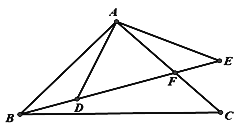
【答案】(1)详见解析;(2)详见解析;(3)18°
【解析】
(1)根据相似三角形的判定定理证明;
(2)根据相似三角形的性质定理得到∠BAC=∠DAE,结合图形,证明即可;
(3)根据相似三角形的性质定理证明.
解:(1)证明:∵![]() ,
,
∴△ABC~△ADE;
(2)∵△ABC~△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAF=∠DAE-∠DAF,
即∠BAD=∠CAE;
(3))∵△ABC~△ADE,
∴∠ABC=∠ADE,
∵∠ABC=∠ABE+∠EBC,∠ADE=∠ABE+∠BAD,
∴∠EBC=∠BAD=18°.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目