题目内容
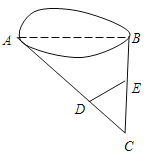
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() ,
,![]() 运动的时间是
运动的时间是![]() (
(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,请说明理由;
值;如果不能,请说明理由;
(2)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
【答案】(1)能,![]() ;(2)
;(2)![]() 或
或![]() 秒时,△DEF为直角三角形
秒时,△DEF为直角三角形
【解析】
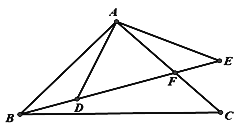
(1)先证得四边形AEFD为平行四边形,若使AEFD为菱形则需要满足的条件即求得;
(2)①∠EDF=90°时,四边形EBFD为矩形.在直角三角形AED中求得AD=2AE即求得;
②∠DEF=90°时,由(2)知EF∥AD,则得∠ADE=∠DEF=90°,求得AD=![]() AE列式即可得.
AE列式即可得.
(1)能.
理由如下:
在△DFC中,∠DFC=90°,∠C=30°,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴AE=DF.
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
又AE=DF,
∴四边形AEFD为平行四边形.
若使AEFD为菱形,则需AE= AD,
![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ;
;
(2)①∠EDF=90°时,四边形EBFD为矩形.
在Rt△AED中,∠ADE=∠C=30°,
∴AD=2AE,
即![]() ,
,
解得:![]() ;
;
②∠DEF=90°时,由(1)知四边形AEFD为平行四边形
∴EF∥AD,
∴∠ADE=∠DEF=90°,
∵∠A+∠C=90°,∠AED+∠A =90°,
∴∠AED=∠C=30°,
∴AD=![]() AE,
AE,
即![]() ,
,
解得:![]() ;
;
③∠EFD=90°时,此种情况不存在;
综上所述,![]() 或
或![]() 秒时,△DEF为直角三角形.
秒时,△DEF为直角三角形.

【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) | 70 | 80 | 90 |
男生(人) | 5 | 10 | 7 |
女生(人) | 4 | 13 | 4 |
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数