Question

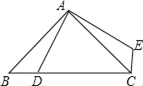
【题目】如图，等腰△ABC内接于⊙O，AB=AC=4，BC=8，则⊙O的半径为___________.

Answer 1

【答案】5cm

【解析】

作AD⊥BC于D，根据等腰三角形的性质得BD=CD=BC=4，再利用三角形外心的定义得到△ABC的外接圆的圆心在AD上，连结OB，设⊙O的半径为r，利用勾股定理，在Rt△ABD中计算出AD=8，然后在Rt△OBD中得到42+（8-r）2=r2，再解关于r的方程即可；

解：

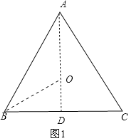
如图1，作AD⊥BC于D，
∵AB=AC，
∴BD=CD=BC=4，
∴△ABC的外接圆的圆心在AD上，
连结OB，设⊙O的半径为r，
在Rt△ABD中，∵AB=4，BD=4，
∴AD= =8，
在Rt△OBD中，OD=AD-OA=8-r，OB=r，BD=4，
∴42+（8-r）2=r2，解得r=5，
即△ABC的外接圆的半径为5；