Question

【题目】已知一次函数．回答下列问题：

（1）求出它的图像与坐标轴的交点坐标；

（2）当自变量满足什么条件时？函数值？

（3）当自变量时，则函数值的范围？

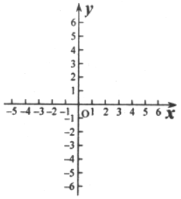
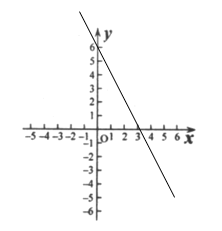
（4）在所给的直角坐标系中，画出直线的图像．

Answer 1

【答案】（1），． （2）当时，． （3）当时，． （4）见解析．

【解析】

（1）分别将和代入中，即可求出交点坐标；

（2）根据，可得y随x的增大而减小，当时，故可得当时，；

（3）根据，可得y随x的增大而减小，当时，当时

故可得当时，；

（4）作出（1）中的交点坐标，作过交点的直线即可．

（1）将代入中

将代入中

解得

故它的图象与坐标轴的交点坐标为和．

（2）∵

∴y随x的增大而减小

∵当时

∴当时，．

（3）∵

∴y随x的增大而减小

∵当时，当时

∴当时，．

（4）如图所示．