题目内容
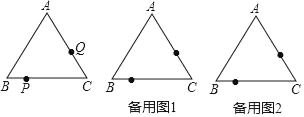
【题目】如图,△ABC是边长为6cm的等边三角形.若点P以1cm/s的速度从点B出发,同时点Q以1.5cm/s的速度从点C出发,都按逆时针方向沿△ABC的边运动,运动时间为6秒.
(1)试求出运动到多少秒时,直线PQ与△ABC的某边平行;
(2)当运动到t1秒时,P、Q对应的点为P1、Q1,当运动到t2秒时(t1≠t2),P、Q对应的点为P2、Q2,试问:△P1CQ1与△P2CQ2能否全等?若能,求出t1、t2的值;若不能,请说明理由.
【答案】(1)当t=2.4或4.8秒时,直线PQ与△ABC的某边平行(2)△P1CQ1与△P2CQ2不全等
【解析】分析:(1)分两种情形,构建方程分别求解即可;
(2)若![]() 与
与![]() 全等,则
全等,则![]() 构建方程组,求出
构建方程组,求出![]() 即可判断;
即可判断;
详解:(1)①如图1中,PQ∥AB时,△PCQ是等边三角形,
∴CP=CQ,
∴6t=1.5t,
t=2.4(秒),
②如图2中,PQ∥AC时,△BPQ是等边三角形,
∴BQ=BP,∵AB=CB,
∴PC=AQ,
∴6t=1.5t6,
∴t=4.8(秒).
综上所述,当t=2.4或4.8秒时,直线PQ与△ABC的某边平行.

(2)如图,若![]() 与
与![]() 全等,则
全等,则![]() ,
,

则有:![]()
解得![]() 不符合题意,
不符合题意,
∴![]() 与
与![]() 不全等;
不全等;

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
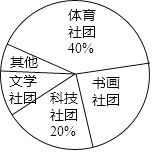
课堂练加测系列答案【题目】某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为 ;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.