题目内容
【题目】点P(t,0)是x轴上的动点,Q(0,2t)是y轴上的动点.若线段PQ与函数y=﹣|x|2+2|x|+3的图象只有一个公共点,则t的取值是_____________.
【答案】![]() ≤t<﹣3或t=
≤t<﹣3或t=![]() 或t≤﹣3
或t≤﹣3
【解析】函数y=-|x|2+2|x|+3的解析式可化为:
y=
设线段PQ所在的直线的解析式为:y=kx+b,
将P(t,0)、Q(0,2t)代入得: ![]() ,解得:
,解得: ![]() ,
,
∴线段PQ所在的直线的解析式为:y=-2x+2t;
①当线段PQ过(0,3)时,即点Q与C重合,如图1,
2t=3,t=![]() ,
,
∴当t=![]() 时,线段PQ与函数y=
时,线段PQ与函数y= 只有一个公共点;
只有一个公共点;
当线段PQ过(3,0)时,即点P与A(3,0)重合,如图2,
t=3,
此时线线段PQ与函数y= 有两个公共点,
有两个公共点,
∴当![]() ≤t<3时,线段PQ与函数y=
≤t<3时,线段PQ与函数y= 只有一个公共点;
只有一个公共点;
②将y=-2x+2t代入y=-x2+2x+3(x≥0)中得,
-x2+2x+3=-2x+2t,
-x2+4x+3-2t=0,
△=16-4×(-1)×(3-2t)=28-8t=0,
t=![]() ,
,
∴当t=![]() 时,线段PQ与函数y=
时,线段PQ与函数y= 也只有一个公共点;
也只有一个公共点;
③当线段PQ过B(-3,0),如图3,即P与B(-3,0)重合,线段PQ只与y=-x2-2x+3(x<0)有一个公共点,此时t=-3,
∴当t≤-3时,线段PQ与函数y=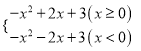 也只有一个公共点;
也只有一个公共点;
综上所述,当线段PQ与函数y=-|x|2+2|x|+3只有一个公共点时,t的取值是![]() ≤t<﹣3或t=
≤t<﹣3或t=![]() 或t≤﹣3,
或t≤﹣3,
故答案为: ![]() ≤t<﹣3或t=
≤t<﹣3或t=![]() 或t≤﹣3.
或t≤﹣3.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目





