��Ŀ����
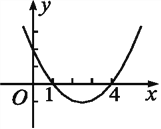
����Ŀ����ͼ��ʾ����֪��ABC�У���B��90�㣬AB��16cm��AC��20cm��P��Q�ǡ�ABC�ı��ϵ��������㣬���е�P�ӵ�A��ʼ��A��B�����˶������ٶ�Ϊÿ��1cm����Q�ӵ�B��ʼ��B��C��A�����˶������ٶ�Ϊÿ��2cm������ͬʱ�������������ʱ��Ϊts��
��1����BC���� ��cm��
��2����tΪ��ֵʱ����P�ڱ�AC�Ĵ�ֱƽ�����ϣ���ʱCQ���� ����
��3������Q�ڱ�CA���˶�ʱ��ֱ��д��ʹ��BCQ��Ϊ���������ε��˶�ʱ�䣮

���𰸡���1��BC��12cm����2��t��![]() ��CQ��13cm����3����tΪ11���12���13.2��ʱ����BCQΪ���������Σ�
��CQ��13cm����3����tΪ11���12���13.2��ʱ����BCQΪ���������Σ�
��������
��1���ɹ��ɶ������ɵó����ۣ�
��2���ɵ�PC��PA��t��PB��16��t����122+��16��t��2��t2�����t��![]() �������CQ��
�������CQ��
��3����t�ֱ��ʾ��BQ��CQ�����õ��������ε����ʿɷ�BQ��BC��CQ��BC��BQ��CQ����������ֱ�õ�����t�ķ��̣������t��ֵ��
�⣺��1���ߡ�B��90����AB��16cm��AC��20cm��
��BC��![]() ��
��![]() ��12��cm����
��12��cm����
�ʴ�Ϊ��12��
��2����ͼ��
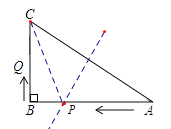
����P�ڱ�AC�Ĵ�ֱƽ�����ϣ�
��PC��PA��t��PB��16��t��
��Rt��BPC��BC2+BP2��CP2����122+��16��t��2��t2��
��ã�t��![]() ��
��
��ʱ����Q�ڱ�AC�ϣ�CQ��![]() ��cm����
��cm����
�ʴ�Ϊ��13cm��
��3������CQ��BQʱ����ͼ1��ʾ��
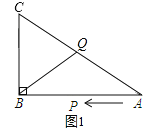
����C����CBQ��
�ߡ�ABC��90����
���CBQ+��ABQ��90����
��A+��C��90����
���A����ABQ��
��BQ��AQ��
��CQ��AQ��10��
��BC+CQ��22��
��2t=22��
��t��22��2��11�룮
����CQ��BCʱ����ͼ2��ʾ��
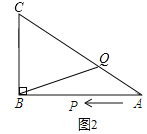
��BC+CQ��24��
��2t=24��
��t��24��2��12�룮
����BC��BQʱ����ͼ3��ʾ��
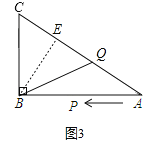
��B����BE��AC�ڵ�E��
��![]() ��
��
��![]() ��
��![]() ��
��
��CQ��2CE��14.4��
��BC+CQ��26.4��
��2t=26.4��
��t��26.4��2��13.2�룮
������������tΪ11���12���13.2��ʱ����BCQΪ���������Σ�

 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�����Ŀ������ɽԺʿ̸����������״��������ʱ˵����������Ҫ���ӷ�������Ҳ���ؿֻţ�������ȥ��Ա�ܼ��ij��������Ŵ����֣�������ע��ͨ�磬��ϴ�֣����˶����ٰ�ҹ����ij����Ϊ�˼�ǿ�������������״����������֪ʶ���˽⣬ͨ����Ⱥ��������״�������ķ���֪ʶ�������������������߲�������2020������״��������ȫ��ͳһ���ԣ�ȫ���������Ծ�����������Ա����Ӽס�������С������ȡ20����Ա�Ĵ���ɼ����������ǵijɼ�����λ���֣�����ͳ�ơ��������������£�
�ռ�����
������85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
������80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
��������
�ɼ�x���֣� | 60��x��70 | 70��x��80 | 80��x��90 | 90��x��100 |
���� | 2 | 5 | a | b |
���� | 3 | 7 | 5 | 5 |
��������
ͳ���� | ƽ���� | ��λ�� | ���� |
���� | 85.75 | 87.5 | c |
���� | 83.5 | d | 80 |
Ӧ������
��1����գ�a���� ����b���� ����c���� ����d���� ����
��2������С������800�˲�����������Ƽ�С���ɼ�����90�ֵ�������
��3����������Ա����ͳ�����ݣ���Ϊ��С��������״����������֪ʶ���ո��ã�����д����������Ա�����ɣ�