题目内容
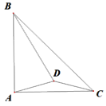
【题目】如图,在直角坐标系中,A(-a,0),B(b,0),C(0,c),且满足![]() .
.
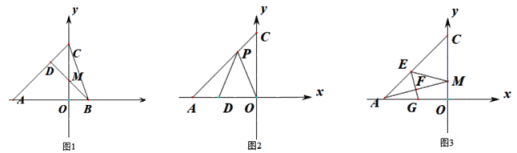
(1)如图1,过B作BD⊥AC,交y轴于M,垂足为D,求M点的坐标.
(2)如图2,若a=3![]() ,AC=6,点P为线段AC上一点,D为x轴负半轴上一点,且PD=PO,∠DPO=45°,求点D的坐标.
,AC=6,点P为线段AC上一点,D为x轴负半轴上一点,且PD=PO,∠DPO=45°,求点D的坐标.
(3)如图3,M在OC上,E在AC上,满足∠CME=∠OMA,EF⊥AM交AO于G,垂足为F,试猜想线段OG,OM,CM三者之间的数量关系,并给出证明.
【答案】(1)M(0,2);(2)D(![]() ,0);(3)OG+OM=CM,证明见解析.
,0);(3)OG+OM=CM,证明见解析.
【解析】
(1)由被开方数大于等于0,可得a=c,b=2,则B点坐标为(2,0),易得△OAC和△OBM为等腰直角三角形,所以OM=OB=2,从而得到M点坐标;
(2)由“一线三等角”模型,易证△PAD≌△OCP,从而得到AP=OC,AD=PC,即可求出OD的长度,进而得到D点坐标;
(3)设OM=m,则M点坐标为(0,m),分别求出AC、AM、EM的解析式,将EM与AC联立求得E点坐标,再根据EF⊥AM,可得EF的斜率,进而求出EF的解析式,然后求出G点坐标即可得出关系.
解:(1)由题意得![]() ,
,
∴![]() ,
,![]()
∴OA=OC,B点坐标(2,0)
∴∠OAC=∠OCA=45°,
又∵BD⊥AC
∴∠OBM=45°,
∴∠OMB=∠OBM=45°,
∴OM=OB=2
∴M点的坐标为(0,2)
(2)∵∠APO=∠APD+∠DPO=∠PCO+∠POC,且∠DPO=∠PCO=45°
∴∠APD=∠POC
在△PAD和△OCP中,
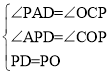
∴△PAD≌△OCP(AAS)
∴AP=OC=![]() ,AD=PC
,AD=PC
∴PC=AC-AP=![]() =AD
=AD
∴OD=OA-AD=![]()
∵D点在x轴负半轴,
∴D点坐标为(![]() ,0)
,0)
(3)OG+OM=CM,证明如下:
设OM=m,则M点坐标为(0,m)
由(1)可知OA=OC=a,A点坐标为(-a,0),C点坐标为(0,a)
∴AC直线解析式为:![]()
AM直线解析式为:![]()
如图,延长EM,AO交于点H,
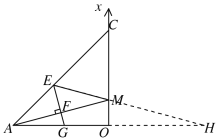
∵∠CME=∠OMA,∠CME=∠OMH
∴∠OMA=∠OMH
又∵MO⊥AH
∴OA=OH=a
∴直线EH解析式为:![]()
将直线AC与直线EH联立得
 解得
解得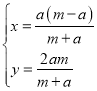
∴E点坐标为(![]() ,
,![]() )
)
∵EF⊥AM
∴kEF·kAM=-1
∴kEF=![]()
设EF解析式为: ![]()
将E点坐标(![]() ,
,![]() )代入得
)代入得
![]() =
=![]() ,解得
,解得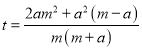
设EF解析式为: 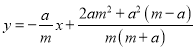
当y=0时,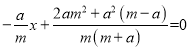
解得![]()
∴G点坐标为(![]() ,0)
,0)
∵G在x轴的负半轴
∴OG=![]()
∴OG+OM=![]()
又∵CM=OC-OM=![]()
∴OG+OM=CM

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案