题目内容
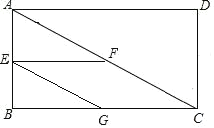
【题目】如图，两个边长分别为a，b（a＞b）的正方形连在一起，三点C，B，F在同一直线上，反比例函数y=
在第一象限的图象经过小正方形右下顶点E．若OB2﹣BE2=8，则k的值是（ ）
A. 3 B. 4 C. 5 D. 4
【答案】B
【解析】
可设E点坐标为（m，n），由四边形OABC与四边形BDEF均为正方形，于是△ABO与△BDE均为等腰直角三角形，结合勾股定理可以表示出OB2与BE2，在结合OB2﹣BE2=8，可得到mn的乘积，即可求出k的值.
解：设E点坐标为（m，n），则AO+DE=m，AB-BD=n，
∵△ABO和△BED都是等腰直角三角形，
∴EB=
BD，OB=AB，BD=DE，OA=AB，
∵OB2-EB2=8，
∴2AB2-2BD2=8，
即AB2-BD2=4，
∴（AB+BD）（AB-BD）=4，
∴（AO+DE）（AB-BD）=4，
∴mn=4，
∴k=4．
故选：B．
练习册系列答案
相关题目
