Question

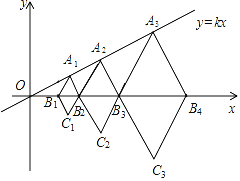
【题目】含60°角的菱形A1B1C1B2，A2B2C2B3，A3B3C3B4，…，按如图的方式放置在平面直角坐标系xOy中，点A1，A2，A3，…，和点B1，B2，B3，B4，…，分别在直线y=kx和x轴上．已知B1（2，0），B2（4，0），则点A1的坐标是_____；点A3的坐标是_____；点An的坐标是____（n为正整数）．

Answer 1

【答案】（3，）， （12，4）， （ ，n）．

【解析】

利用菱形的性质得出△A1B1B2是等边三角形，进而得出A1坐标，进而得出OB2=A2B2=4，即可得出A3，An的坐标．

解： 过点A1作A1D⊥x轴于点D，

∵含60°角的菱形A1B1C1B2，A2B2C2B3，A3B3C3B4，…，

∴∠A1B1D=60°，A1B1=A1B2，

∴△A1B1B2是等边三角形，

∵B1（2，0），B2（4，0），

∴A1B1=B1B2=2，

∴B1D=1，A1D=，∴OD=3，

则A1（3，），

∴tan∠A1OD=，

∴∠A1OD=30°，

∴OB2=A2B2=4，

同理可得出：A2（6，2），则A3（12，4），

则点An的坐标是：（ ，n）．

故答案为（3，），（12，4），（ ，n）．