题目内容
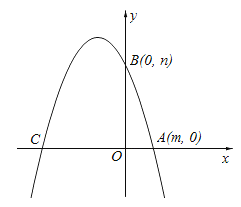
【题目】如图,在平面直角坐标系中,抛物线 y=ax2﹣5ax+c 交 x 轴于点 A,点 A 的坐标为(4,0).
(1)用含 a 的代数式表示 c.
(2)当 a=![]() 时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
(3)当 a=![]() 时,求 0≤x≤6 时 y 的取值范围.
时,求 0≤x≤6 时 y 的取值范围.
(4)已知点 B 的坐标为(0,3),当抛物线的顶点落在△AOB 外接圆内部时,直接写出 a的取值范围.
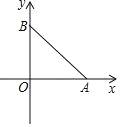
【答案】(1)c=4a;(2)当 x=![]() 时,y 取得最小值,最小值为﹣
时,y 取得最小值,最小值为﹣![]() ;(3)当 0≤x≤6 时,y 的取值范围是﹣5≤y≤
;(3)当 0≤x≤6 时,y 的取值范围是﹣5≤y≤![]() ;(4)-
;(4)-![]() ﹣
﹣![]() <a<﹣
<a<﹣![]() +
+![]() 且 a≠0.
且 a≠0.
【解析】
(1)由抛物线和x轴的交点A的坐标代入即可求出
(2)已知a的值可求出c的值,从而可以求出抛物线的解析式;再把抛物线的解析式用配方法表示出来,根据抛物线的性质特点求出
(3)已知a的值求出b,从而求出抛物线的解析式;把抛物线用配方法表示出来根据其性质可求出y的取值范围
(4)把抛物线的解析式用配方法表示出来求出其对称轴和定点坐标,根据题意作出圆在进行分析解答
(1)将 A(4,0)代入 y=ax2﹣5ax+c,得:16a﹣20a+c=0,解得:c=4a.
(2)当 a=![]() 时,c=2,
时,c=2,
∴抛物线的解析式为 y=![]() x2﹣
x2﹣ ![]() x+2=
x+2=![]() (x﹣
(x﹣![]() )2﹣
)2﹣ ![]() .
.
∵a= ![]() >0,
>0,
∴当 x=![]() 时,y 取得最小值,最小值为﹣
时,y 取得最小值,最小值为﹣![]() .
.
(3)当 a=﹣![]() 时,c=﹣2,
时,c=﹣2,
∴抛物线的解析式为 y=﹣![]() x2+
x2+ ![]() x﹣2=﹣
x﹣2=﹣![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() .
.
∵a=﹣![]() <0,
<0,
∴当 x=![]() 时,y 取得最大值,最大值为
时,y 取得最大值,最大值为![]() ; 当 x=0 时,y=﹣2;
; 当 x=0 时,y=﹣2;
当 x=6 时,y=﹣![]() ×62+
×62+ ![]() ×6﹣2=﹣5.
×6﹣2=﹣5.
∴当 0≤x≤6 时,y 的取值范围是﹣5≤y≤![]() .
.
(4)∵抛物线的解析式为 y=ax2﹣5ax+4a=a(x﹣![]() )2﹣
)2﹣ ![]() a,
a,
∴抛物线的对称轴为直线 x=![]() ,顶点坐标为(
,顶点坐标为(![]() ,﹣
,﹣![]() a).
a).
设线段 AB 的中点为 O,以 AB 为直径作圆,设抛物线对称轴与⊙O 交于点 C,D,过点 O
作 OH⊥CD 于点 H,如图所示.
∵点 A 的坐标为(4,0),点 B 的坐标(0,3),
∴AB=5,点 O 的坐标为(2,![]() ),点 H 的坐标为(
),点 H 的坐标为(![]() ,
,![]() ).在 Rt△COH 中,
).在 Rt△COH 中,
OC=![]() AB=
AB= ![]() ,OH=
,OH= ![]() ,
,
∴CH= ![]() ,
,
∴点 C 的坐标为(![]() ,
,![]() ).
).
同理:点 D 的坐标为(![]() ,﹣
,﹣![]() ),
),
∴ ![]()
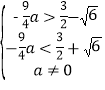
![]() ,
,
解得:﹣![]() -
-![]() <a<﹣
<a<﹣![]() +
+![]() 且 a≠0.
且 a≠0.