题目内容
【题目】用一段长32m的篱笆和长8m的墙,围成一个矩形的菜园.
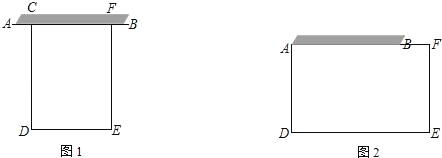
(1)如图1,如果矩形菜园的一边靠墙AB,另三边由篱笆CDEF围成
①设DE等于xm,直接写出菜园面积y与x之间的函数关系式,并写出自变量的取值范围;
②菜园的面积能不能等于110m2?若能,求出此时x的值;若不能,请说明理由;
(2)如图2,如果矩形菜园的一边由墙AB和一节篱笆BF构成,另三边由篱笆ADEF围成,求菜园面积的最大值.
【答案】(1)①y=﹣![]() x2+16x(0<x≤8) ②不能 0<x≤8 (2)100
x2+16x(0<x≤8) ②不能 0<x≤8 (2)100![]()
【解析】
(1)①首先设DE等于xm,则DC=![]() (32﹣x)m,进而利用矩形面积公式得出答案;
(32﹣x)m,进而利用矩形面积公式得出答案;
②利用一元二次方程的解法结合①中自变量取值范围得出答案;
(2)首先表示出AD的长,再利用矩形面积公式求出答案.
解:(1)①由题意可得:设DE等于xm,则DC=![]() (32﹣x)m,
(32﹣x)m,
故菜园面积y与x之间的函数关系式为:y=![]() (32﹣x)x=﹣
(32﹣x)x=﹣![]() x2+16x,(0<x≤8);
x2+16x,(0<x≤8);
②若菜园的面积等于110m2,则﹣![]() x2+16x=110.
x2+16x=110.
解得:x1=10,x2=22.
因为0<x≤8,所以不能围成面积为110m2的菜园.
(2)设DE等于xm,则菜园面积为:
y=![]() x(32+8﹣2x)
x(32+8﹣2x)
=-x2+20x
=-(x﹣10)2+100,
当x=10时,函数有最大值100.
答:当DE长为10m时,菜园的面积最大,最大值为100m2.
故答案为:(1)①y=﹣![]() x2+16x(0<x≤8), ②不能;(2)100
x2+16x(0<x≤8), ②不能;(2)100![]() .
.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目