题目内容
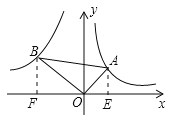
【题目】如图,已知第一象限内的点A在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA=![]() ,则k的值为( )
,则k的值为( )

A. -3 B. -6 C. -4 D. -![]()
【答案】C
【解析】过A作AE⊥x轴,过B作BF⊥x轴,由OA与OB垂直,再利用邻补角定义得到一对角互余,再由直角三角形BOF中的两锐角互余,利用同角的余角相等得到一对角相等,又一对直角相等,利用两对对应角相等的三角形相似得到三角形BOF与三角形OEA相似,在直角三角形AOB中,由锐角三角函数定义,根据cos∠BAO的值,设出AB与OA,利用勾股定理表示出OB,求出OB与OA的比值,即为相似比,根据面积之比等于相似比的平方,求出两三角形面积之比,由A在反比例函数y=![]() 上,利用反比例函数比例系数的几何意义求出三角形AOE的面积,进而确定出BOF的面积,再利用k的集合意义即可求出k的值.
上,利用反比例函数比例系数的几何意义求出三角形AOE的面积,进而确定出BOF的面积,再利用k的集合意义即可求出k的值.
过A作AE⊥x轴,过B作BF⊥x轴.
∵OA⊥OB,∴∠AOB=90°,∴∠BOF+∠EOA=90°.
∵∠BOF+∠FBO=90°,∴∠EOA=∠FBO.
∵∠BFO=∠OEA=90°,∴△BFO∽△OEA.在Rt△AOB中,cos∠BAO=![]() =
=![]() .
.
设AB=![]() ,则OA=1,根据勾股定理得:BO=
,则OA=1,根据勾股定理得:BO=![]() ,∴OB:OA=
,∴OB:OA=![]() :1,
:1,
∴S△BFO:S△OEA=2:1.
∵A在反比例函数y=![]() 上,∴S△OEA=1,∴S△BFO=2,则k=﹣4.
上,∴S△OEA=1,∴S△BFO=2,则k=﹣4.
故选C.

【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.