Question

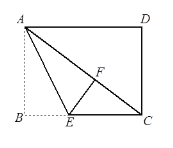
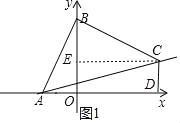
【题目】如图，在平面鱼角坐标系xOy中，A（﹣3，0），点B为y轴正半轴上一点，将线段AB绕点B旋转90°至BC处，过点C作CD垂直x轴于点D，若四边形ABCD的面积为36，则线AC的解析式为_____．

Answer 1

【答案】y＝x+1或y＝﹣3x﹣9．

【解析】

过C作CE⊥OB于E，则四边形CEOD是矩形，得到CE＝OD，OE＝CD，根据旋转的性质得到AB＝BC，∠ABC＝90°，根据全等三角形的性质得到BO＝CE，BE＝OA，求得OA＝BE＝3，设OD＝a，得到CD＝OE＝|a﹣3|，根据面积公式列方程得到C（﹣6，9）或（6，3），设直线AB的解析式为y＝kx+b，把A点和C点的坐标代入即可得到结论．

解：过C作CE⊥OB于E，

则四边形CEOD是矩形，

∴CE＝OD，OE＝CD，

∵将线段AB绕点B旋转90°至BC处，

∴AB＝BC，

∠ABC＝90°，

∴∠ABO+∠CBO＝∠CBO+∠BCE＝90°，

∴∠ABO＝∠BCE，

∵∠AOB＝∠BEC＝90°，

∴△ABO≌△BCO（AAS），

∴BO＝CE，BE＝OA，

∵A（﹣3，0），

∴OA＝BE＝3，

设OD＝a，

∴CD＝OE＝|a﹣3|，

∵四边形ABCD的面积为36，

∴AOOB+（CD+OB）OD＝×3×a+（a﹣3+a）×a＝36，

∴a＝±6，

∴C（﹣6，9）或（6，3），

设直线AB的解析式为y＝kx+b，

把A点和C点的坐标代入得， 或

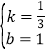解得：或 ，

∴直线AB的解析式为或y＝﹣3x﹣9．

故答案为：或y＝﹣3x﹣9．