题目内容
【题目】如图,已知AM∥BN,∠B=40°,点P是BN上一动点(与点B不重合).AC、AD分别平分∠BAP和∠PAM,交射线BN于点C、D.

(1)求∠CAD的度数;
(2)当点P运动到当∠ACB=∠BAD时,求∠BAC的度数.
【答案】(1)∠CAD=70°;(2)=35°
【解析】
(1)由平行线的性质,角平分线的定义,角的和差求得∠CAD的度数为70°;
(2)由平行线的性质,角平分线的定义,已知等量关系求得∠BAC的度数为35°.
如图所示:
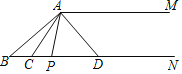
(1)∵AM∥BN,
∴∠B+∠BAM=180°,
又∵∠B=40°,
∴∠BAM=180°﹣∠B=140°,
又∵AC、AD分别平分∠BAP和∠PAM,
∴∠CAP=![]() ∠BAP,∠PAD=
∠BAP,∠PAD=![]() ∠PAM,
∠PAM,
∴∠CAP+∠PAD=![]() (∠BAP+∠PAM)
(∠BAP+∠PAM)
=![]() ∠BAM
∠BAM
=![]()
=70°
又∵∠CAD=∠CAP+∠PAD,
∴∠CAD=70°;
(2)∵AM∥BN,
∴∠ACB=∠MAC,
又∵∠ACB=∠BAD,
∴∠MAC=∠BAD,
∴∠MAC﹣∠DAC=∠BAD﹣∠DAC,
∴∠MAD=∠BAC
又∵AC,AD分别平分∠BAP和∠PAM,
∴∠BAC=∠CAP,∠MAD=∠PAD
∴∠BAC=∠CAP=∠MAD=∠PAD
又∵∠BAM=140°
∴∠BAC=![]() ∠BAM=
∠BAM=![]() ×140°=35°.
×140°=35°.

 计算高手系列答案
计算高手系列答案【题目】某电器商场销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是该型号电风扇近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
![]() 求A、B两种型号的电风扇的销售单价;
求A、B两种型号的电风扇的销售单价;
![]() 若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?