��Ŀ����
����Ŀ����ͼ���Գ���Ϊֱ��x= ![]() �������߾�����A��6��0����B��0��4����
�������߾�����A��6��0����B��0��4����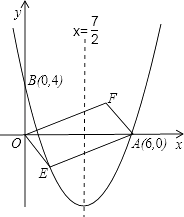
��1���������߽���ʽ���������ꣻ
��2�����E��x��y������������һ���㣬��λ�ڵ������ޣ��ı���OEAF����OAΪ�Խ��ߵ�ƽ���ı��Σ���ƽ���ı���OEAF�����S��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
�ٵ�ƽ���ı���OEAF�����Ϊ24ʱ�����ж�ƽ���ı���OEAF�Ƿ�Ϊ���Σ�
���Ƿ���ڵ�E��ʹƽ���ı���OEAFΪ�����Σ������ڣ������E�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��Ϊ�����ߵĶԳ�����x= ![]() ��
��
�����ʽΪy=a��x�� ![]() ��2+k��
��2+k��
��A��B�������������ʽ���� 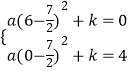 ��
��
���a= ![]() ��k=��
��k=�� ![]() ��
��
�������߽���ʽΪy= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��������
�������� ![]() ����
���� ![]() ��
��
��2��
�⣺�ߵ�E��x��y�����������ϣ�λ�ڵ������ޣ��������ʺ�y= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
��y��0��
����y��0����y��ʾ��E��OA�ľ��룮
��OA��OEAF�ĶԽ��ߣ�
��S=2S��OAE=2�� ![]() ��OA|y|=��6y=��4��x��
��OA|y|=��6y=��4��x�� ![]() ��2+25��
��2+25��
��Ϊ��������x������������ǣ�1��0���ͣ�6��0����
�����Ա���x��ȡֵ��Χ��1��x��6��
�� �������⣬��S=24ʱ������4��x�� ![]() ��2+25=24��
��2+25=24��
���ã�x�� ![]() ��2=
��2= ![]() ��
��
���x1=3��x2=4��
������ĵ�E��������
�ֱ�ΪE1��3����4����E2��4����4����
��E1��3����4������OE=AE��
����ƽ���ı���OEAF�����Σ�
��E2��4����4��������OE=AE��
����ƽ���ı���OEAF�������Σ�
�ڵ�OA��EF����OA=EFʱ��ƽ���ı���OEAF�������Σ�
��ʱ��E������ֻ���ǣ�3����3����
������Ϊ��3����3���ĵ㲻���������ϣ�
�ʲ����������ĵ�E��ʹƽ���ı���OEAFΪ������
����������1����֪�������ߵĶԳ������ʽ�����ö���ʽ���κ���ͨʽ���������ߣ�Ȼ��A��B�������������⼴�ɣ���2��ƽ���ı��ε����Ϊ������OEA�����2������˿ɸ���E��ĺ����꣬�������ߵĽ���ʽ���E��������꣬��ôE��������ľ���ֵ��Ϊ��OAE�ĸߣ��ɴ˿ɸ��������ε������ʽ�ó���AOE�������x�ĺ�����ϵʽ�����ɵó�S��x�ĺ�����ϵʽ��
�ٽ�S=24����S��x�ĺ�����ϵʽ�����x��ֵ�����ɵó�E��������OE��OA�ij������ƽ���ı���OEAF�����Σ���������ƽ���ı����������ߵij���ȣ��ݴ˿��жϳ��ı���OEAF�Ƿ�Ϊ���Σ�
������ı���OEAF�������Σ���ô������OEAӦ���ǵ���ֱ�������Σ���E�������Ϊ��3����3��������������ߵĽ���ʽ�м����жϳ��Ƿ���ڷ���������E�㣮

 �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�����Ŀ��ijСѧ���꼶�����꼶��ȫ��ѧ���μӡ����ǡ�֪ʶ���ԣ������10�⣬ÿ��10�֣����������ȡ�˲���ѧ���ijɼ�����ͳ�ƣ����ֳ���ѧ��ÿ�����ٴ����6�⣬�ֽ��й�������������Ƴ����¡��꼶����ͳ��ͼ������δȫ����ɵġ��ɼ����ͳ�Ʊ�����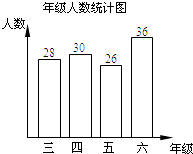
�ɼ����ͳ�Ʊ�
�ɼ� | 100�� | 90�� | 80�� | 70�� | 60�� |
���� | 21 | 40 | 5 | ||
Ƶ�� | 0.3 |
����ͼ�����ṩ����Ϣ���ش��������⣺
��1���뽫ͳ�Ʊ���������
�ɼ����ͳ�Ʊ�
�ɼ� | 100�� | 90�� | 80�� | 70�� | 60�� |
���� | 21 | 40 | 5 | ||
Ƶ�� | 0.3 |
��2������ѧ���У��ɼ�Ϊ80�ֵ�ѧ�������� ���������� �֣���λ���� �֣�
��3������Сѧ���꼶�����꼶����1800��ѧ������ɹ��Ƴ��ɼ�Ϊ70�ֵ�ѧ������Լ�� ����



