题目内容
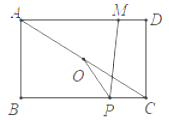
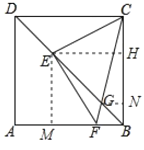
【题目】如图,在正方形 ABCD 中,AB=6,点 E 在对角线 BD 上,DE=![]() ,连接 CE,过点 E作 EF⊥CE,交线段 AB 于点 F
,连接 CE,过点 E作 EF⊥CE,交线段 AB 于点 F
(1)求证:CE=EF;
(2)求 FB 的长;
(3)连接 FC 交 BD 于点 G.求 BG 的长.

【答案】(1)见解析(2)4(3)![]()
【解析】
(1)过E作EM⊥AB于M,EH⊥BC于H,根据正方形的性质得到∠EBM=∠HBE=45![]() ,求得EM=EH,根据全等三角形的性质即可得到结论;
,求得EM=EH,根据全等三角形的性质即可得到结论;
(2)根据勾股定理得到BD=6![]() ,得到AM=CH=1,根据全等三角形的性质得到FM=CH=1,于是得到结论;
,得到AM=CH=1,根据全等三角形的性质得到FM=CH=1,于是得到结论;
(3)过G作GN⊥BC于N,设GN=BN=x,根据相似三角形的性质即可得到结论.
(1)过E作EM⊥AB于M,EH⊥BC于H,
∵四边形ABCD是正方形,
∴∠EBM=∠HBE=45![]() ,
,
∴EM=EH,
∵∠EMB=∠MBH=∠BHE=90![]() ,
,
∴∠MEH=90![]() ,
,
∵EF⊥CE,
∴∠CEF=90![]() ,
,
∴∠MEF=∠CEH,
∴△EMF≌△EHC(ASA),
∴CE=EF;
(2)∵AB=6,
∴BD=6![]() ,
,
∵DE=![]() ,
,
∴BE=BDDE=5![]() ,
,
∵BM2+EM2=BE2,BM=EM
∴BM=BH=5,
∴AM=CH=1,
∵△EMF≌△EHC,
∴FM=CH=1,
∴BF=ABAMMF=611=4;
(3)过G作GN⊥BC于N,
∴GN=BN,
设GN=BN=x,
∴CN=6x,
∵GN⊥BC,AB⊥BC,
∴GN∥BF,
∴△CGN∽△CFB,
∴![]() ,
,
∴![]() ,
,
∴x=![]() ,
,
∴BN=GN=![]() ,
,
∴BG=![]() .
.

练习册系列答案
相关题目