题目内容
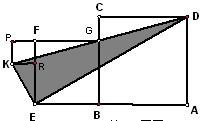
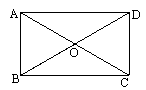
如图,矩形ABCD中,AB=8,AD=10.
(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
②点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处, 求线段CT长度的最大值与最小值之和。

(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
②点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处, 求线段CT长度的最大值与最小值之和。

(1)36
(2)①∵四边形ABCD是矩形,
由折叠对称性:AF=AD=10,FE=DE.
在Rt△ABF中,BF=6. ∴FC=4.
在Rt△ECF中,42+(8-DE)2=EF2,解得DE=5.
②分三种情形讨论:
若AP=AF,∵AB⊥PF,∴PB=BF=6.
若PF=AF,则PB+6=10,解得PB=4.
若AP=PF,在Rt△APB中,AP2=PB2+AB2,解得PB=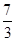 .
.
综合得PB=6或4或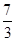 .
.
(3)当点N与C重合时,AT取最大值是8,
当点M与A重合时, AT取最小值为4.
所以线段AT长度的最大值与最小值之和为:12.
(2)①∵四边形ABCD是矩形,
由折叠对称性:AF=AD=10,FE=DE.
在Rt△ABF中,BF=6. ∴FC=4.
在Rt△ECF中,42+(8-DE)2=EF2,解得DE=5.
②分三种情形讨论:
若AP=AF,∵AB⊥PF,∴PB=BF=6.
若PF=AF,则PB+6=10,解得PB=4.
若AP=PF,在Rt△APB中,AP2=PB2+AB2,解得PB=
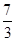 .
. 综合得PB=6或4或
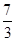 .
.(3)当点N与C重合时,AT取最大值是8,
当点M与A重合时, AT取最小值为4.
所以线段AT长度的最大值与最小值之和为:12.
(1)因为矩形的两组对边相等,所以周长等于邻边之和的2倍;
(2)①四边形ABCD是矩形,由折叠对称的特点和勾股定理即可求出ED的长;
②分若AP=AF;PF=AF以及AP=P三种情形分别讨论求出满足题意的PB的值即可;
(4)由题意可知当点N与C重合时,AT取最大值是8,当点M与A重合时,AT取最小值为4,进而求出
线段CT长度的最大值与最小值之和.
(2)①四边形ABCD是矩形,由折叠对称的特点和勾股定理即可求出ED的长;
②分若AP=AF;PF=AF以及AP=P三种情形分别讨论求出满足题意的PB的值即可;
(4)由题意可知当点N与C重合时,AT取最大值是8,当点M与A重合时,AT取最小值为4,进而求出
线段CT长度的最大值与最小值之和.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目

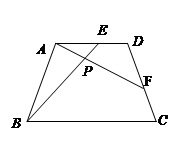

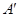 处,折痕为PQ,当点
处,折痕为PQ,当点
 ;
; 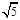 ;
;  .
.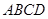 、正方形
、正方形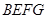 和正方形
和正方形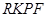 的位置如图所示,点
的位置如图所示,点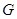 在线段
在线段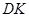 上,已知
上,已知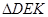 的面积为 .
的面积为 .