题目内容
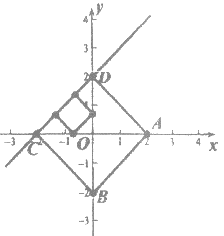
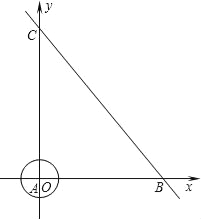
【题目】如图,在直角坐标系中,半径为1的⊙A圆心与原点O重合,直线l分别交x轴、y轴于点B、C,点B的坐标为(6,0),∠ABC=60°.
(1)若点P是⊙A上的动点,则P到直线BC的最小距离是 .
(2)若点A从原点O出发,以1个单位/秒的速度沿着线路OB→BC→CO运动,回到点O停止运动,⊙A随着点A的运动而移动.设点A运动的时间为t.
①求⊙A在整个运动过程中与坐标轴相切时t的取值;
②求⊙A在整个运动过程中所扫过的图形的面积.
【答案】(1)P到直线BC的最小距离是3![]() ﹣1;(2)①t的值是1秒或(6+
﹣1;(2)①t的值是1秒或(6+![]() )秒或16秒或(17+6
)秒或16秒或(17+6![]() )秒;②10
)秒;②10![]() +33+π.
+33+π.
【解析】
(1)作高线AG,利用点B的坐标为(6,0),根据直角三角形30度角的性质及勾股定理可得AE和PE的长;
(2)①利用切线的性质和特殊三角函数可得对应t的值即可,注意利用数形结合得出.
②利用⊙A在整个运动过程中所扫过的面积=矩形DROC面积+矩形OYHB面积+矩形BGFC面积+△ABC面积+一个圆的面积﹣△LSK面积,求出即可.
解:(1)如图1,∵点B的坐标为(6,0),
∴OB=6,
∵∠CAB=90°,∠ABC=60°,
过A作AG⊥BC于G,交⊙A于P,此时P到直线BC的距离最小,
∴∠EAB=30°,
∴BE=![]() OB=3,
OB=3,
∴![]()
∵AP=1,
∴![]()
则P到直线BC的最小距离是![]() ;
;
故答案为:![]() ;
;
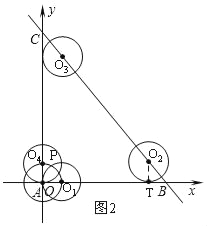
(2)①如图2所示:⊙A在整个运动过程中与坐标轴相切有4种不同的情况,
∵∠OCB=30°,OB=6,
∴BC=12, ![]()
当⊙O1与y轴相切于点O,可知:t=OO1=1;
同理可得:OO4=1,
此时t=6+12+![]() ﹣1=17+
﹣1=17+![]() ;
;
当⊙O2与x轴相切于点T,
∴O2T=1,∠OBC=60°,
∴sin60°=![]() ,
,
∴![]()
∴O2B=![]() ,
,
∴![]() ,
,
同理可得:当⊙O3与y轴相切时,t=6+12﹣2=16;
综上所述,当⊙A在整个运动过程中与坐标轴相切时,t的值是1秒或(![]() )秒或16秒或(17+6
)秒或16秒或(17+6![]() )秒;
)秒;
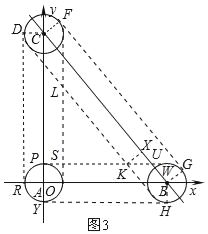
②如图3所示:当圆分别在O,B,C位置时,作出公切线DR,YH,FG,PW,切点分别为:D,R,H,G,F,P,W
连接CD,CF,BG,过点K作KX⊥BC于点X,PW交BC于点U,
∵PU∥OB,
∴∠OBC=∠KUX,
∵∠KXU=∠COB=90°,
∴△COB∽△KXU,
∵KX=1,BC=12,
∴![]()
∴![]()
解得:KU=![]() ,
,
∵PU∥BO,
∴△CPU∽△COB,
∴![]()
∴![]()
解得: ![]()
则![]()
同理可得出:△LSK∽△COB,
∴![]()
∴![]()
解得:![]()
则∠CDR=∠CFG=∠BGF=∠BHY=∠AYH=90°,
故⊙A在整个运动过程中所扫过的面积
=矩形DROC面积+矩形OYHB面积+矩形BGFC面积+△ABC面积+一个圆的面积﹣△LSK面积
![]()
![]()


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案