题目内容
【题目】在一个不透明的口袋里装有分别标有数字﹣3、﹣1、0、2的四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)从中任取一球,求抽取的数字为正数的概率;
(2)从中任取一球,将球上的数字记为a,求关于x的一元二次方程ax2﹣2ax+a+3=0有实数根的概率;
(3)从中任取一球,将球上的数字作为点的横坐标,记为x(不放回);再任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第二象限内的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)四个数字中正数有一个,求出所求概率即可;
(2)表示出已知方程根的判别式,根据方程有实数根求出a的范围,即可求出所求概率;
(3)列表得出所有等可能的情况数,找出点(x,y)落在第二象限内的情况数,即可求出所求的概率.
试题解析:解:(1)根据题意得:抽取的数字为正数的情况有1个,则P=![]() ;
;
(2)∵方程ax2﹣2ax+a+3=0有实数根,
∴△=4a2﹣4a(a+3)=﹣12a≥0,且a≠0,
解得:a<0,
则关于x的一元二次方程ax2﹣2ax+a+3=0有实数根的概率为![]() ;
;
(3)列表如下:
﹣3 | ﹣1 | 0 | 2 | |
﹣3 | ﹣﹣﹣ | (﹣1,﹣3) | (0,﹣3) | (2,﹣3) |
﹣1 | (﹣3,﹣1) | ﹣﹣﹣ | (0,﹣1) | (2,﹣1) |
0 | (﹣3,0) | (﹣1,0) | ﹣﹣﹣ | (2,0) |
2 | (﹣3, | (﹣1,2) | (0,2) | ﹣﹣﹣ |
所有等可能的情况有12种,其中点(x,y)落在第二象限内的情况有2种,
则P=![]() =
=![]() .
.

 考前必练系列答案
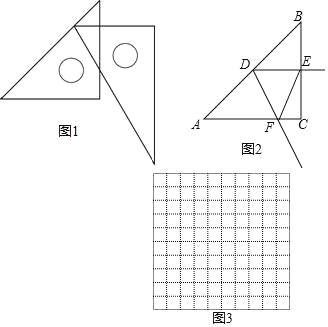
考前必练系列答案【题目】在数学活动课上,老师提出了一个问题:把一副三角尺如图1摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?
小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.下面是小林的探究过程,请补充完整:
(1)画出几何图形,明确条件和探究对象;
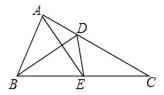
如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=_____°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | ____ | 4.5 | 6 |
(说明:补全表格时相关数据保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为_____cm.