题目内容
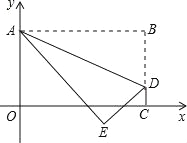
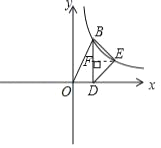
【题目】如图,在平面直角坐标系中,O为坐标原点,直角三角形OBD的直角顶点D在x轴正半轴上,B在第一象限,OB=![]() ,tan∠BOD=2.
,tan∠BOD=2.
(1)求图象经过点B的反比例函数的解析式.
(2)点E是(1)中反比例函数图象上一点,连接BE、DE,若BE=DE,求四边形OBED的面积.

【答案】(1)y=![]() ;(2)8.
;(2)8.
【解析】
(1)设OD=m,则BD=2m,OB=![]() =
=![]() m,求得B点坐标,代入反比例函数的解析式为y=
m,求得B点坐标,代入反比例函数的解析式为y=![]() ,解得k即可;
,解得k即可;
(2)作EF⊥BD于F,由BD⊥x轴,则∠EFD=∠ODF,易得F(2,2),可得E点坐标,利用三角形的面积公式可得结果.
(1)解:在直角三角形OBD中,tan∠BOD=![]() =2.
=2.
∴BD=2OD,
设OD=m,则BD=2m,OB=![]() =
=![]() m,
m,
∵OB=2![]() ,
,
∴![]() m=2
m=2![]() ,
,
∴m=2
∴OD=2,BD=4.
∴B(2,4),
设反比例函数的解析式为y=![]() ,把B(2,4)代入得k=8,
,把B(2,4)代入得k=8,
∴图象经过点B的反比例函数的解析式为y=![]() ;
;
(2)作EF⊥BD于F,由BD⊥x轴,
∴∠EFD=∠ODF,
∴EF∥x轴,
∵BE=DE,EF⊥BD于F,
∴BF=DF=![]() =2,
=2,
∴F(2,2),
∴E点纵坐标为2,令![]() =2,
=2,
∴x=4,
∴E(4,2),EF=2,
∴S四边形OBED=S△OBD+S△BDE![]()

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目