Question

【题目】如图，AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB交弧BC于点D，连接CD、OD，给出以下四个结论：①AC∥OD；②CE=OE；③△ODE∽△ADO；④2CD2=CEAB．其中正确结论的序号是 ．

Answer 1

【答案】①④
【解析】解：①∵AB是半圆直径， ∴AO=OD，
∴∠OAD=∠ADO，
∵AD平分∠CAB交弧BC于点D，
∴∠CAD=∠DAO= ∠CAB，
∴∠CAD=∠ADO，
∴AC∥OD，
∴①正确．
②过点E作EF⊥AC，
∵OC⊥AB，AD平分∠CAB交弧BC于点D，
∴OE=EF，
在Rt△EFC中，CE＞EF，
∴CE＞OE，
∴②错误．
③∵在△ODE和△ADO中，只有∠ADO=∠EDO，
∵∠COD=2∠CAD=2∠OAD，
∴∠DOE≠∠DAO，
∴不能证明△ODE和△ADO相似，
∴③错误；
④∵AD平分∠CAB交弧BC于点D，
∴∠CAD= ×45°=22.5°，
∴∠COD=45°，
∵AB是半圆直径，
∴OC=OD，
∴∠OCD=∠ODC=67.5°
∵∠CAD=∠ADO=22.5°（已证），
∴∠CDE=∠ODC﹣∠ADO=67.5°﹣22.5°=45°，
∴△CED∽△CDO，
∴ ，
∴CD2=OCCE= ABCE，
∴2CD2=CEAB．
∴④正确．
综上所述，只有①④正确．
所以答案是：①④．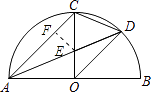

【考点精析】根据题目的已知条件，利用三角形的内角和外角和等腰三角形的判定的相关知识可以得到问题的答案，需要掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角；如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等．