题目内容
如图1,直线AB:y=-| 3 |
| 3 |
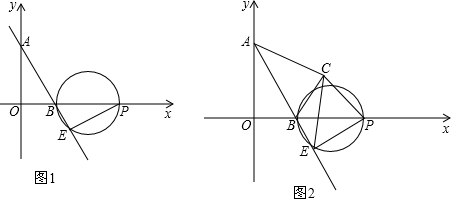
(1)求∠ABO的度数.
(2)当t=5时,求BE的长.
(3)如图2将△AOB沿直线AB翻折180°,得到△ABC.
①求点C的坐标.
②探究:当t取何值时,△EPC和△AOB相似.
分析:(1)先由直线AB的解析式求A、B两点的坐标,再根据锐角三角函数值求∠ABO的度数;
(2)由∠EBP=∠ABO,已知BP,解直角三角形EBP求BE;
(3)①过点C作CM⊥OA于M,在直角三角形ACM中,已知AC及∠CAM的度数,根据锐角三角函数即可求出点C的坐标;
②要使△EPC和△AOB相似,而△AOB是有一个角为30°的直角三角形,只需△EPC也是有一个角为30°的直角三角形.由于∠CEP<∠BEP=90°,所以有可能∠CPE=90°或者∠PCE=90°,然后分情况讨论.
(2)由∠EBP=∠ABO,已知BP,解直角三角形EBP求BE;
(3)①过点C作CM⊥OA于M,在直角三角形ACM中,已知AC及∠CAM的度数,根据锐角三角函数即可求出点C的坐标;
②要使△EPC和△AOB相似,而△AOB是有一个角为30°的直角三角形,只需△EPC也是有一个角为30°的直角三角形.由于∠CEP<∠BEP=90°,所以有可能∠CPE=90°或者∠PCE=90°,然后分情况讨论.
解答:解:(1)∵直线AB:y=-
x+
与y轴、x轴交于A、B两点,
∴A(0,
),B(1,0).
在直角△AOB中,∵tan∠ABO=
=
,
∴∠ABO=60°;
(2)当t=5时,BP=4,
在直角△EBP中,∠BEP=90°,∠EBP=∠ABO=60°,
∴BE=
BP=2;
(3)①过点C作CM⊥OA于M.
 ∵将△AOB沿直线AB翻折180°,得到△ABC,
∵将△AOB沿直线AB翻折180°,得到△ABC,
∴△AOB≌△ACB,
∴∠OAB=∠CAB=30°,AO=AC=
,
∴∠MAC=60°.
在直角三角形ACM中,∠AMC=90°,AC=
,∠CAM=60°,
∴CM=
,AM=
,
∴OM=OA-AM=
.
∴点C的坐标为(
,
);
②∵△EPC和△AOB相似,∠CEP<∠BEP=90°,
∴可能∠CPE=90°或者∠PCE=90°,且△EPC有一个角为30°.
设E(x,-
x+
),点P的坐标为(t,0).
过点E作EN⊥OP于N,由射影定理,得EN2=BN•NP,
即(-
x+
)2=(x-1)(t-x),
整理,得t=4x-3.
分如下几种情况:
第一种:如果∠CPE=90°,∠CEP=30°,那么CP=
CE,
即
=
,
整理,得20x2-46x+27=0,
∵△=(-46)2-4×20×27<0,
∴原方程无解;
第二种:如果∠CPE=90°,∠ECP=30°,那么EP=
CE,
即
=
,
整理,得44x2-90x+45=0,
∵△=(-90)2-4×44×45=180,
∴x=
,
∴t=4x-3=
,
又∵t>1,
∴t=
;
第三种:如果∠PCE=90°,∠CEP=30°,那么CP=
PE,
即
=
,
整理,得13x2-30x+18=0,
∵△=(-30)2-4×13×18<0,
∴原方程无解;
第四种:如果∠PCE=90°,∠CPE=30°,那么CE=
PE,
即
=
,
整理,得x2=0,
∴x=0,
∴t=4x-3=-3,不合题意舍去,
∴原方程无解.
综上,可知当t=
时,△EPC和△AOB相似.
| 3 |
| 3 |
∴A(0,
| 3 |
在直角△AOB中,∵tan∠ABO=
| OA |
| OB |
| 3 |
∴∠ABO=60°;
(2)当t=5时,BP=4,
在直角△EBP中,∠BEP=90°,∠EBP=∠ABO=60°,
∴BE=
| 1 |
| 2 |
(3)①过点C作CM⊥OA于M.
 ∵将△AOB沿直线AB翻折180°,得到△ABC,
∵将△AOB沿直线AB翻折180°,得到△ABC,∴△AOB≌△ACB,
∴∠OAB=∠CAB=30°,AO=AC=
| 3 |
∴∠MAC=60°.
在直角三角形ACM中,∠AMC=90°,AC=
| 3 |
∴CM=
| 3 |
| 2 |
| ||
| 2 |
∴OM=OA-AM=
| ||
| 2 |
∴点C的坐标为(
| 3 |
| 2 |
| ||
| 2 |
②∵△EPC和△AOB相似,∠CEP<∠BEP=90°,
∴可能∠CPE=90°或者∠PCE=90°,且△EPC有一个角为30°.
设E(x,-
| 3 |
| 3 |
过点E作EN⊥OP于N,由射影定理,得EN2=BN•NP,
即(-
| 3 |
| 3 |
整理,得t=4x-3.
分如下几种情况:
第一种:如果∠CPE=90°,∠CEP=30°,那么CP=
| 1 |
| 2 |

即
(t-
|
| 1 |
| 2 |
(x-
|
整理,得20x2-46x+27=0,
∵△=(-46)2-4×20×27<0,
∴原方程无解;
第二种:如果∠CPE=90°,∠ECP=30°,那么EP=
| 1 |
| 2 |
即
(t-x)2+(
|
| 1 |
| 2 |
(x-
|
整理,得44x2-90x+45=0,
∵△=(-90)2-4×44×45=180,
∴x=
45±3
| ||
| 44 |
∴t=4x-3=
12±3
| ||
| 11 |
又∵t>1,
∴t=
12+3
| ||
| 11 |
第三种:如果∠PCE=90°,∠CEP=30°,那么CP=
| 1 |
| 2 |
即
(t-
|
| 1 |
| 2 |
(t-x)2+(
|
整理,得13x2-30x+18=0,
∵△=(-30)2-4×13×18<0,
∴原方程无解;
第四种:如果∠PCE=90°,∠CPE=30°,那么CE=
| 1 |
| 2 |
即
(x-
|
| 1 |
| 2 |
(t-x)2+(
|
整理,得x2=0,
∴x=0,
∴t=4x-3=-3,不合题意舍去,
∴原方程无解.
综上,可知当t=
12+3
| ||
| 11 |
点评:本题主要考查了一次函数,直角三角形、全等三角形、相似三角形的知识,综合性强,有一定难度.运用分类讨论的思想解决最后一问是解题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
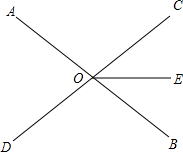 如图2,直线AB与CD相交于一点O,OE平分∠COB,且∠AOE=140°,则∠AOC=( )
如图2,直线AB与CD相交于一点O,OE平分∠COB,且∠AOE=140°,则∠AOC=( ) 如图,若直线AB∥ED,你能推得∠B、∠C、∠D之间的数量关系吗?请说明理由.
如图,若直线AB∥ED,你能推得∠B、∠C、∠D之间的数量关系吗?请说明理由.
 如图,若直线AB∥ED,你能推得∠ABC,∠BCD,∠CDE之间的数量关系吗?请说明理由.
如图,若直线AB∥ED,你能推得∠ABC,∠BCD,∠CDE之间的数量关系吗?请说明理由.