题目内容
已知:如图1,直线AB∥CD,EF分别交AB、CD于E、F两点,∠BEF、∠DFE的平分线相交于点K.
(1)求∠EKF的度数.(计算过程不准用三角形内角和)
(2)如图2,∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.
(3)在图2中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,作∠BEKn、∠DFKn的平分线相交于点Kn+1,请用含的n式子表示∠Kn+1的度数.(直接写出答案,不必写解答过程)

(1)求∠EKF的度数.(计算过程不准用三角形内角和)
(2)如图2,∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.
(3)在图2中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,作∠BEKn、∠DFKn的平分线相交于点Kn+1,请用含的n式子表示∠Kn+1的度数.(直接写出答案,不必写解答过程)

分析:(1)过K作KG∥AB,可得KG∥CD,可得出两对内错角相等,由EK与FK分别为角平平分线,利用角平分线定义得到两对角相等,再由AB与CD平行,利用两直线平行同旁内角互补得到两对角互补,利用等式的性质求出∠BKE+∠DFK的度数,即可求出∠EKF的度数;
(2)∠K=2∠K1,由∠BEK、∠DFK的平分线相交于点K1,利用角平分线定义得到两对角相等,等量代换求出∠K1,进而确定出两角的关系;
(3)依此类推即可确定出∠Kn+1的度数.
(2)∠K=2∠K1,由∠BEK、∠DFK的平分线相交于点K1,利用角平分线定义得到两对角相等,等量代换求出∠K1,进而确定出两角的关系;
(3)依此类推即可确定出∠Kn+1的度数.
解答: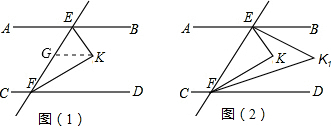
解:(1)过K作KG∥AB,可得KG∥CD,
∴∠BEK=∠EKG,∠GKF=∠KFD,
∵EK、FK分别为∠BEF与∠EFD的平分线,
∴∠BEK=∠FEK,∠EFK=∠DFK,
∵AB∥CD,
∴∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠DFK)=180°,
∴∠BEK+∠DFK=90°,
则∠EKF=∠EKG+∠GKF=90°;
(2)∠K=2∠K1,理由为:
∵∠BEK、∠DFK的平分线相交于点K1,
∴∠BEK1=∠KEK1,∠KFK1=∠DFK1,
∵∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠KFD)=180°,
∴∠BEK+∠KFD=90°,即∠KEK1+∠KFK1=45°,
∴∠K1=180°-(∠KEF+∠EFK)-(∠KEK1+∠KFK1)=45°,
则∠K=2∠K1;
(3)归纳总结得:∠Kn+1=
×90°.

解:(1)过K作KG∥AB,可得KG∥CD,
∴∠BEK=∠EKG,∠GKF=∠KFD,
∵EK、FK分别为∠BEF与∠EFD的平分线,
∴∠BEK=∠FEK,∠EFK=∠DFK,
∵AB∥CD,
∴∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠DFK)=180°,
∴∠BEK+∠DFK=90°,
则∠EKF=∠EKG+∠GKF=90°;
(2)∠K=2∠K1,理由为:
∵∠BEK、∠DFK的平分线相交于点K1,
∴∠BEK1=∠KEK1,∠KFK1=∠DFK1,
∵∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠KFD)=180°,
∴∠BEK+∠KFD=90°,即∠KEK1+∠KFK1=45°,
∴∠K1=180°-(∠KEF+∠EFK)-(∠KEK1+∠KFK1)=45°,
则∠K=2∠K1;
(3)归纳总结得:∠Kn+1=
| 1 |
| 2n+1 |
点评:此题考查了平行线的性质,角平分线定义,属于探究型试题,熟练掌握平行线的性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
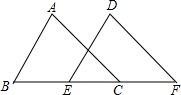 已知:如图,同一直线上有四点B、E、C、F,且∠A=∠D,∠B=∠DEF,BE=CF.
已知:如图,同一直线上有四点B、E、C、F,且∠A=∠D,∠B=∠DEF,BE=CF.
 已知:如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等(要求写出作法,并保留作图痕迹,写出结论)
已知:如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等(要求写出作法,并保留作图痕迹,写出结论)