题目内容
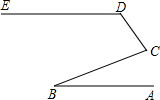如图，若直线AB∥ED，你能推得∠ABC，∠BCD，∠CDE之间的数量关系吗？请说明理由．分析：首先过点C作CF∥DE，由AB∥ED，可得AB∥DE∥CF，然后由平行线的性质，即可得∠1+∠CDE=180°，∠2=∠ABC，继而求得答案．
解答：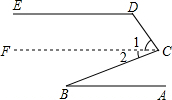
解：∠BCD+∠CDE-∠ABC=180°．
理由：过点C作CF∥DE，
∵AB∥ED，
∴AB∥DE∥CF，
∴∠1+∠CDE=180°，∠2=∠ABC，
∵∠1+∠2=∠BCD，
∴∠BCD+∠CDE-∠ABC=180°．
解：∠BCD+∠CDE-∠ABC=180°．理由：过点C作CF∥DE，
∵AB∥ED，
∴AB∥DE∥CF，
∴∠1+∠CDE=180°，∠2=∠ABC，
∵∠1+∠2=∠BCD，
∴∠BCD+∠CDE-∠ABC=180°．
点评：此题考查了平行线的性质．此题难度不大，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
相关题目
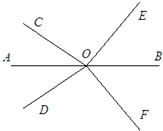21、如图，若直线AB分别平分∠COD和∠EOF．
如图，若直线AB分别平分∠COD和∠EOF．