题目内容
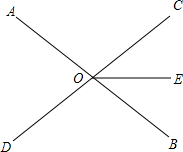 如图2,直线AB与CD相交于一点O,OE平分∠COB,且∠AOE=140°,则∠AOC=( )
如图2,直线AB与CD相交于一点O,OE平分∠COB,且∠AOE=140°,则∠AOC=( )分析:根据角平分线的定义得到∠COE=
∠COB,根据平角的定义得∠AOC+∠COB=180°,则
∠AOC+∠COE=90°,由∠AOE=140°,即∠AOC+∠COE=140°得到∠COE=140°-∠AOC,
则
∠AOC+140°-∠AOC=90°,再解方程即可.
| 1 |
| 2 |
| 1 |
| 2 |
则
| 1 |
| 2 |
解答:解:∵OE平分∠COB,
∴∠COE=
∠COB,
∵∠AOC+∠COB=180°,
∴
∠AOC+∠COE=90°,
∵∠AOE=140°,即∠AOC+∠COE=140°,
∴∠COE=140°-∠AOC,
∵∠AOE=140°,即∠AOC+∠COE=140°,
∴∠COE=140°-∠AOC,
∴
∠AOC+140°-∠AOC=90°,
∴∠AOC=100°.
故选C.
∴∠COE=
| 1 |
| 2 |
∵∠AOC+∠COB=180°,
∴
| 1 |
| 2 |
∵∠AOE=140°,即∠AOC+∠COE=140°,
∴∠COE=140°-∠AOC,
∵∠AOE=140°,即∠AOC+∠COE=140°,
∴∠COE=140°-∠AOC,
∴
| 1 |
| 2 |
∴∠AOC=100°.
故选C.
点评:本题考查了角平分线的性质:从角的顶点引一条射线,把这个角分成相等的两部分,那么这条射线叫这个角的平分线.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
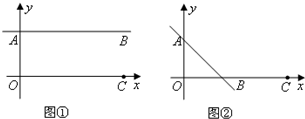
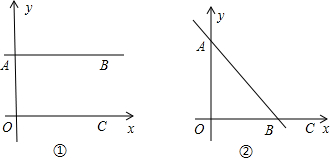
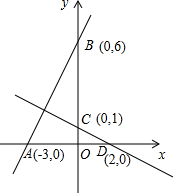 点A,B,C,D的坐标如图,求直线AB与直线CD的交点坐标.
点A,B,C,D的坐标如图,求直线AB与直线CD的交点坐标.