题目内容
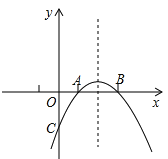
【题目】已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB=1的点P有几个?并求出所有点P的坐标;
(3)设抛物线交y轴于点C,问该抛物线对称轴上是否存在点M,使得△MAC的周长最小?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】【答案(1)抛物线解析式为![]() ;
;
(2)满足条件的点P有三个坐标分别为(2,1),(![]() ,﹣1),(
,﹣1),(![]() ,﹣1);
,﹣1);
(3)存在点M(2,﹣1),可使△AMC的周长最小.
【解析】
(1)将A(1,0),B(3,0)代入抛物线![]() 中,列方程组可求抛物线解析式;
中,列方程组可求抛物线解析式;
(2)由于AB=3﹣1=2,而![]() ,故△PAB中,AB边上的高为1,即P点纵坐标为±1,代入抛物线解析式可求P点横坐标;
,故△PAB中,AB边上的高为1,即P点纵坐标为±1,代入抛物线解析式可求P点横坐标;
(3)过点C作抛物线的对称轴的对称点C',根据抛物线的对称性求得C′(4,﹣3),连接直线AC′,求直线AC′的解析式,直线AC′与对称轴的交点即为所求点M
解:(1)依题意有![]() ,
,
∴b=4,c=﹣3,
∴抛物线解析式为![]() ;
;
(2)如图,设P(x,y)
∵AB=2,![]()
∴![]() ×2×|y|=1
×2×|y|=1
∴y=±1
当y=1时,![]() 解得
解得![]() ,
,
当y=﹣1时,![]() 解得
解得![]() ,
,
∴满足条件的点P有三个坐标分别为(2,1),(![]() ,﹣1),(
,﹣1),(![]() ,﹣1);
,﹣1);
(3)存在.
过点C作抛物线的对称轴的对称点C',如图
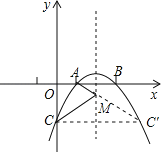
∵点C(0,﹣3),对称轴为x=2,
∴C′(4,﹣3),
设直线AC′的解析式为y=kx+b,
则![]() ,
,
∴k=﹣1,b=1,
∴直线AC′的解析式为y=﹣x+1,
直线AC′与对称轴x=2的交点为(2,﹣1),即M(2,﹣1),
∴存在点M(2,﹣1),可使△AMC的周长最小.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目





