题目内容
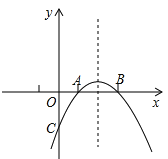
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①9a﹣3b+c=0;②4a﹣2b+c>0;③方程ax2+bx+c﹣4=0有两个相等的实数根;④方程a(x﹣1)2+b(x﹣1)+c=0的两根是x1=﹣2,x2=2.其中正确结论的个数是_________.

【答案】4
【解析】
①根据x=-3时,对应的y=0,代入可得结论;
②根据x=-2时,对应的y>0,代入可得结论;
③根据顶点坐标中y=4,可得方程ax2+bx+c-4=0有两个相等的实数根;
④将x-1替换x,由方程ax2+bx+c=0的两根x1=-3,x2=1,可得结论.
解:①由抛物线的对称性可知:与x轴交于另一点为(-3,0),
∴9a-3b+c=0;
故①正确;
②由图象得:当x=-2时,y>0,
∴4a-2b+c>0,
故②正确;
③∵抛物线的顶点(-1,4),
∴方程ax2+bx+c=4有两个相等的实数根,
即方程ax2+bx+c-4=0有两个相等的实数根;
故③正确;
④由题意得:方程ax2+bx+c=0的两根为:x1=-3,x2=1,
∴方程a(x-1)2+b(x-1)+c=0的两根是:x-1=-3或x-1=1,
∴x1=-2,x2=2,
故④正确;
综上得:正确结论为: 4个.

 阅读快车系列答案
阅读快车系列答案【题目】为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛,某学校组织了一次体育知识竞赛.每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图,如图所示.
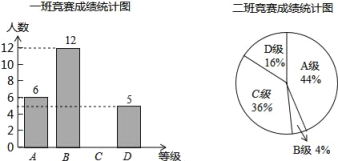
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
平均数(分) | 中位数(分) | 众数(分) | 方差 | |
一班 | a | b | 90 | 106.24 |
二班 | 87.6 | 80 | c | 138.24 |
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.