题目内容
【题目】如图,已知BC∥GE,AF∥DE,∠1=56°.
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=14°,求∠ACB的度数.
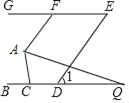
【答案】(1)56°,(2)84°.
【解析】
(1)先根据BC∥EG得出∠E=∠1=56°,再由AF∥DE可知∠AFG=∠E=56°;
(2)作AM∥BC,由平行线的传递性可知AM∥EG,故∠FAM=∠AFG,再根据AM∥BC可知∠QAM=∠Q,故∠FAQ=∠FAM+∠QAM,再根据AQ平分∠FAC可知∠MAC=∠QAC+∠QAM=84°,根据AM∥BC即可得出结论.
(1)∵BC∥EG,
∴∠E=∠1=56°.
∵AF∥DE,
∴∠AFG=∠E=56°;
(2)作AM∥BC,
∵BC∥EG,
∴AM∥EG,
∴∠FAM=∠AFG=56°.
∵AM∥BC,
∴∠QAM=∠Q=14°,
∴∠FAQ=∠FAM+∠QAM=70°.
∵AQ平分∠FAC,
∴∠QAC=∠FAQ=70°,
∴∠MAC=∠QAC+∠QAM=84°.
∵AM∥BC,
∴∠ACB=∠MAC=84°.

练习册系列答案
相关题目