题目内容
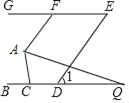
【题目】如图，已知：AD平分∠CAE，AD∥BC．
（1）求证：△ABC是等腰三角形．
（2）当∠CAE等于多少度时△ABC是等边三角形？证明你的结论．
【答案】（1）证明见解析；（2）当∠CAE=120°时，△ABC是等边三角形，证明见解析.
【解析】试题分析：
（1）由已知条件易得∠EAD=∠CAD，∠EAD=∠B，∠CAD=∠C，从而可得∠B=∠C，进一步可得AB=AC，由此即可得到△ABC是等腰三角形；
（2）由（1）可知△ABC是等腰三角形，因此当∠BAC=60°，即∠CAE=120°时，△ABC是等边三角形.
试题解析：
（1）∵AD平分∠CAE，
∴∠EAD=∠CAD，
∵AD∥BC，
∴∠EAD=∠B，∠CAD=∠C，
∴∠B=∠C，
∴AB=AC．
故△ABC是等腰三角形．
（2）当∠CAE=120°时，△ABC是等边三角形，理由如下：
∵∠CAE=120°，
∴∠BAC=180°-∠CAE=180°-120°=60°，
又∵AB=AC，
∴△ABC是等边三角形．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
