ЬтФПФкШн
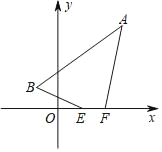
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЁбCЕФАыОЖЮЊrЃЌЕуPЪЧгыдВаФCВЛжиКЯЕФЕуЃЌИјГіШчЯТЖЈвхЃКШєЕуPЁфЮЊЩфЯпCPЩЯвЛЕуЃЌТњзуCPCPЁф=r2 ЃЌ дђГЦЕуPЁфЮЊЕуPЙигкЁбCЕФЗДбнЕуЃЎгвЭМЮЊЕуPМАЦфЙигкЁбCЕФЗДбнЕуPЁфЕФЪОвтЭМЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЁбOЕФАыОЖЮЊ1ЪБЃЌЗжБ№ЧѓГіЕуMЃЈ1ЃЌ0ЃЉЃЌNЃЈ0ЃЌ2ЃЉЃЌTЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЙигкЁбOЕФЗДбнЕуMЁфЃЌNЁфЃЌTЁфЕФзјБъЃЛ
ЃЉЙигкЁбOЕФЗДбнЕуMЁфЃЌNЁфЃЌTЁфЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌвбжЊЕуAЃЈ1ЃЌ4ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌвдABЮЊжБОЖЕФЁбGгыyжсНЛгкЕуCЃЌDЃЈЕуCЮЛгкЕуDЯТЗНЃЉЃЌEЮЊCDЕФжаЕуЃЎ
ЂйШєЕуOЃЌEЙигкЁбGЕФЗДбнЕуЗжБ№ЮЊOЁфЃЌEЁфЃЌЧѓЁЯEЁфOЁфGЕФДѓаЁЃЛ
ЂкШєЕуPдкЁбGЩЯЃЌЧвЁЯBAP=ЁЯOBCЃЌЩшжБЯпAPгыxжсЕФНЛЕуЮЊQЃЌЕуQЙигкЁбGЕФЗДбнЕуЮЊQЁфЃЌЧыжБНгаДГіЯпЖЮGQЁфЕФГЄЖШЃЎ
ЁОД№АИЁПНтЃКЃЈ1ЃЉЁпONONЁф=1ЃЌON=2ЃЌ
ЁрONЁф=![]() ЃЌЁрЗДбнЕуNЁфзјБъЃЈ0ЃЌ
ЃЌЁрЗДбнЕуNЁфзјБъЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпOMOMЁф=1ЃЌOM=1ЃЌ
ЁрOMЁф=1
ЗДбнЕуMЁфзјБъЃЈ1ЃЌ0ЃЉ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпTЁфдкЕквЛЯѓЯоЕФНЧЦНЗжЯпЩЯЃЌ
ЁрЗДбнЕуTЁфзјБъЃЈ1ЃЌ1ЃЉ
ЃЈ2ЃЉЂйгЩЬтвтЃКAB=2![]() ЃЌr=
ЃЌr=![]() ЃЌ
ЃЌ
ЁпEЃЈ0ЃЌ2ЃЉЃЌGЃЈ2ЃЌ2ЃЉЃЌEG=2ЃЌEЁфGEG=5ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпOGOЁфG=5ЃЌOG=2![]() ЃЌ
ЃЌ
ЁрOЁфG=![]() ЃЌ
ЃЌ
ЁпEЁфЃЈЉ![]() ЃЌ2ЃЉЃЌOЁфЃЈ
ЃЌ2ЃЉЃЌOЁфЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрOЁфEЁф=![]() ЃЌ
ЃЌ
ЁрEЁфG2=EЁфOЁф2+OЁфG2 ЃЌ
ЁрЁЯEЁфOЁфG=90Ёу
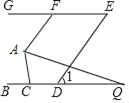
ЂкШчЭМЃКЁпЁЯBAP1=ЁЯOBCЃЌЁЯCAP1+ЁЯCBP1=ЁЯCAB+ЁЯBAP1+ЁЯCBP1=180ЁуЃЌЁЯOBC+ЁЯCBP1+ЁЯP1BQ1=180ЁуЃЌЁЯCAB=45ЁуЃЌ
ЁрЁЯP1BQ1=45ЁуЃЌ
ЁпЁЯAP1B=ЁЯBP1Q1=90ЁуЃЌ
ЁрЁїPBQ1ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
гЩЁїAP1BЁзЁїBOCЕУЕНЃК![]() =3ЃЌ
=3ЃЌ
ЁпAB=2![]() ЃЌ
ЃЌ
ЁрBP1=![]() ЃЌBQ1=2ЃЌQ1ЃЈ5ЃЌ0ЃЉЃЌ
ЃЌBQ1=2ЃЌQ1ЃЈ5ЃЌ0ЃЉЃЌ
ЁпQ1ЁфGGQ1=5ЃЌ
ЁрQ1ЁфG=![]() ЃЌ
ЃЌ
ЁпЁЯP2AB=ЁЯBAP1ЃЌ
ЁрP1 ЃЌ P2ЙигкжБЯпABЖдГЦЃЌЁпP1ЃЈ4ЃЌ1ЃЉЃЌвзжЊЃКP2ЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЁржБЯпAP2ЃКY=Љ7X+11ЃЌЁрQ2ЃЈ![]() ,0ЃЉЃЌ
,0ЃЉЃЌ
гЩЃКQ2ЁфGQ2G=5ЕУЕНЃКQ2ЁфG=![]() ЃЎ
ЃЎ
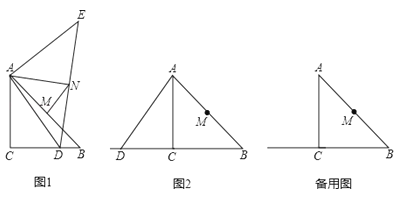
ЁОНтЮіЁПЃЈ1ЃЉРћгУЗДбнЕуЖЈвхЃЌЯШЧѓГіЃКONЁфЃЌOTЁфЃЌOMЁфЕФГЄЖШЃЌШЛКѓЧѓГіЫќУЧЕФзјБъЃЛ
ЃЈ2ЃЉЂйЧѓГіЃКEЁфGЃЌOЁфGЃЌOЁфEЁфЃЌРћгУЙДЙЩЖЈРэФцЖЈРэжЄУїЁїEЁфOЁфGЪЧRTЁїЃЛ
ЂкПМТЧСНжжЧщаЮЃЌЕуPдкжБЯпABзѓгвЖМДцдкЃЎ

 КЎМйДДаТаЭзджїбЇЯАЕкШ§бЇЦкКЎМйЯЮНгЯЕСаД№АИ
КЎМйДДаТаЭзджїбЇЯАЕкШ§бЇЦкКЎМйЯЮНгЯЕСаД№АИ