题目内容
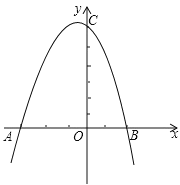
【题目】已知二次函数![]() 的图像如图所示.
的图像如图所示.
(1)当![]() 时,说明这个二次函数的图像与x轴必有两个交点;
时,说明这个二次函数的图像与x轴必有两个交点;
(2)如图情况下,若![]() ,求点C的坐标.
,求点C的坐标.
【答案】(1)证明见详解
(2)C的坐标是(0,6)
【解析】
(1)根据求得△值,再根据△>0来判断二次函数的图象与x轴必有两个交点;
(2)将求二次函数y=-x2+(m-2)x+3(m+1)与x轴的交点转化为求方程-x2+(m-2)x+3(m+1)=0的解,再根据一元二次方程根与系数的关系,可求得m的值,再将m的值代入二次函数.由图中不难发现C点是二次函数与x轴的交点,令x=0,求得y的值.至此C点坐标确定.
解:(1)∵△=(m-2)2-4(-1)3(m+1)=(m+4)2
∵![]()
∴△=(m+4)2>0,
∴抛物线与x轴必有两个交点;
(2)设方程![]() 的两根为x1、x2,且x1<0,x2>0
的两根为x1、x2,且x1<0,x2>0
由图可知![]() ,由
,由![]() ,可知
,可知![]()
根据根与系数的关系,可知![]() ,
,
则m=1,于是二次函数的解析式为![]() ,
,
把x=0代入![]() ,得y=6,
,得y=6,
所以C的坐标是(0,6).

练习册系列答案
相关题目