Question

【题目】四边形ABCD中，AB=BC，∠B=∠C=90°，P是BC边上一点，AP⊥PD，E是AB边上一点，∠BPE=∠BAP．

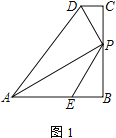
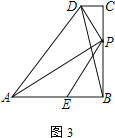
（1） 如图1，若AE=PE，直接写出=______；

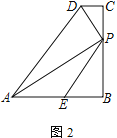
（2） 如图2，求证：AP=PD＋PE；

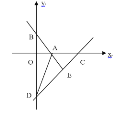
（3） 如图3，当AE=BP时，连BD，则=______，并说明理由．

Answer 1

【答案】（1）；（2）证明见解析；（3）．

【解析】

（1）首先证明∠PAB=30°，设PB=a，可得AB=BCa，求出PC即可解决问题；

（2）如图2中，延长DP交AB的延长线于M，作MN⊥DC交DC的延长线于N．首先证明PE=PM，再证明△ABP≌△MND（ASA）即可解决问题；

（3）如图3，延长DP交AB的延长线于M，作MN⊥DC交DC的延长线于N．首先证明DN=PB=AE，EB=BM=CN，设AE=PB=DN=x，EB=BM=CN=y，求出PE，BD即可解决问题．

（1）如图1．

∵AE=PE，∴∠EAP=∠EPA．

∵∠EPB=∠PAE，∴∠EPB=∠PAE=∠EPA．

∵∠B=90°，∴∠PAB+∠APB=90°，∴3∠PAE=90°，∴∠PAE=30°．

设PB=a，则AB=BCa，∴PC=BC﹣PBa﹣a，∴1．

故答案为：．

（2）如图2，延长DP交AB的延长线于M，作MN⊥DC交DC的延长线于N．

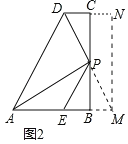
∵AP⊥DM，∴∠APM=∠PBM=90°．

∵∠PAE+∠APB=90°，∠APB+∠BPM=90°，∴∠PAE=∠BPM．

∵∠EPB=∠PAE，∴∠EPB=∠BPM．

∵∠EPB+∠PEB=90°，∠BPM+∠PMB=90°，∴∠PEB=∠PMB，∴PE=PM．

∵∠CBM=∠BCN=∠N=90°，∴四边形BCNM是矩形，∴BC=MN=AB，BC∥MN，∴∠DMN=∠BPM=∠PAB．

∵∠ABP=∠N=90°，∴△ABP≌△MND（ASA），∴PA=DM．

∵DM=DP+PM=DP+PE，∴PA=DP+PE．

（3）如图3，延长DP交AB的延长线于M，作MN⊥DC交DC的延长线于N．

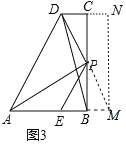
由（2）可知：PE=PM，△ABP≌△MND，四边形BCNM是矩形，∴PB=DN，设PB=DN=x，∴AE=PB=DN=x．

∵PE=PM，PB⊥EM，∴EB=BM．

∵BM=CN，∴BE=BM=CN，设BE=BM=CN=y，则CD=x﹣y，BC=AB=x+y．

在Rt△PBE中，PE．在Rt△DCB中，BD，∴．

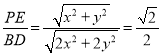故答案为：．