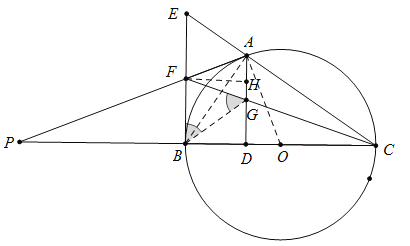
题目内容
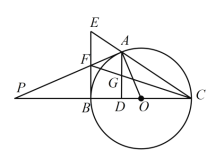
【题目】如图,点 ![]() 是以
是以 ![]() 为直径的
为直径的 ![]() 上一点,
上一点,![]() 于点
于点 ![]() ,过点
,过点 ![]() 作
作 ![]() 的切线,与
的切线,与 ![]() 的延长线相交于点
的延长线相交于点 ![]() ,
,![]() 是
是 ![]() 的中点,连接
的中点,连接 ![]() 并延长与
并延长与 ![]() 相交于点
相交于点 ![]() ,延长
,延长 ![]() 与
与 ![]() 的延长线相交于点
的延长线相交于点 ![]() ,且
,且 ![]() .
.
(1)求证:BF=EF;
(2)求![]() ;
;
(3)求![]() 的半径r.
的半径r.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
(1)根据AD∥EB得到△CAG∽△CEF,△CGD∽△CFB,根据相似三角形对应边成比例即可得到结论;
(2)求出AH,FH的值,根据tan∠P=tan∠AFH=![]() =
=![]() =
=![]() ,即可解决问题;
,即可解决问题;
(3)在Rt△ADO中利用勾股定理即可求出半径.
(1)∵EB 是切线,AD⊥BC,
∴∠EBC=∠ADC=90°,
∴AD∥ EB,
∴△CAG∽△CEF,△CGD∽△CFB,
∴![]() .
.
∵AG=GD,
∴EF=FB.
(2)连接AB.过点F作FH⊥AG交AG于点H.
∵BC 是直径,
∴∠BAC=∠BAE=90°.
∵EF=FB,
∴FA=FB=FE=FG=3(直角三角形斜边上的中线等于斜边的一半).
∵FA=FG,FH⊥AG,
∴AH=HG.
∵∠FBD=∠BDH=∠FHD=90°,
∴ 四边形 FBDH 是矩形,
∴FB=DH=3.
∵AG=GD,
∴AH=HG=1,GD=2,FH=![]() .
.
∵FH∥PD,
∴∠AFH=∠APD,
∴tanP=tan∠AFH=![]() .
.
(3)设半径为 r,在 Rt△ADO 中,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.

 金牌教辅培优优选卷期末冲刺100分系列答案
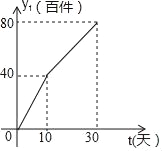
金牌教辅培优优选卷期末冲刺100分系列答案【题目】我市红领服饰有限公司生产了一款夏季服装,通过实验商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示:
时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量yt(百件) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y1与t的函数关系式及自变量t的取值范围;
(2)网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的关系如图所示.求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.