题目内容
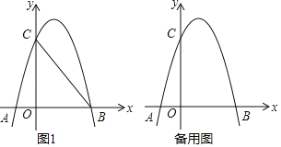
【题目】若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数.
(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1,和y2=x2+bx+c,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求当0≤x≤3时,y2的取值范围.
【答案】(1) y=(x-1)2+3和y=2(x-1)2+3(答案不唯一);(2)y2 =x2 -2x+1,0![]() .
.
【解析】
(1)根据“同簇二次函数”的定义写出两个即可;
(2)将A代入y1=2x24mx+2m2+1中,可求出y1与x的函数关系式,并求出此抛物线的顶点坐标,从而求出y1+y2与x的函数关系式,再根据“同簇二次函数”的定义即可求出b、c,从而求出函数y2的表达式,最后根据二次函数的性质自变量的取值范围和对称轴的位置关系求最值即可.
(1)根据“同簇二次函数”的定义:两个二次函数图象的顶点,开口方向都相同,
故这两个二次函数可以为:y=(x-1)2+3和y=2(x-1)2+3;
(2)把A(1,1)代入y1=2x24mx+2m2+1得24m+2m2+1=1,
解得m=1,则y1=2x24x+3=2(x-1)2+1,
∴y1=2x24x+3顶点坐标为(1,1),且y1+y2=3x2+(b4)x+c+3
∵y1+y2与y1为“同簇二次函数”
∴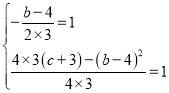
解得:b=-2,c=1
y2 =x2 -2x+1
此抛物线的开口向上,对称轴为:![]()
∴0≤x≤3包含对称轴
∴当![]() 时,y2取最小值,此时y2=0,当x=3时,y2取最大值,此时y2=4
时,y2取最小值,此时y2=0,当x=3时,y2取最大值,此时y2=4
∴0![]()

【题目】某校开展校园“美德少年”评选活动,共有“助人为乐”,“自强自立”、“孝老爱亲”,“诚实守信”四种类别,每位同学只能参评其中一类,评选后,把最终入选的20位校园“美德少年”分类统计,制作了如下统计表,后来发现,统计表中前两行的数据都是正确的,后两行的数据中有一个是错误的.
类别 | 频数 | 频率 |
助人为乐美德少年 | a | 0.20 |
自强自立美德少年 | 3 | b |
孝老爱亲美德少年 | 7 | 0.35 |
诚实守信美德少年 | 6 | 0.32 |
根据以上信息,解答下列问题:
(1)统计表中的a= ,b ;
(2)统计表后两行错误的数据是 ,该数据的正确值是 ;
(3)校园小记者决定从A,B,C三位“自强自立美德少年”中随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率.
【题目】某校在“校园体育文化节”活动中组织了“球类知识我知道”的竞赛活动,从初三年级1200名学生中随机抽查了100名学生的成绩(满分30分),整理得到如下的统计图表:
成绩(分) | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
频率统计表
成绩分组 | 频数 | 频率 |
15≤x<18 | 3 | 0.03 |
18≤x<21 | a | 0.12 |
21≤x<24 | 20 | 0.20 |
24≤x<27 | 35 | 0.35 |
27≤x≤30 | 30 | b |
频数分布直方图
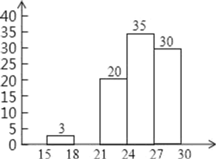
请根据所提供的信息解答下列问题:
(1)样本的众数是 分,中位数是 分;
(2)频率统计表中a= ,b= ;补全频数分布直方图;
(3)请根据抽样统计结果,估计该次竞赛中初三年级成绩不少于21分的大约有多少人?随机抽取一名同学的成绩,其值不小于24分的概率是多少?