题目内容
如图，四边形ABCD 中，AD=CD ，∠DAB= ∠ACB=90°，过点D做DE⊥AC，垂足为F，DE与AB相交于点E
（1）求证：AB·AF=CB·CD
（2）已知：AB=15cm，BC=9cm，P是射线DE上的动点，设DP=xcm(x>0)，四边形BCDP的面积为y㎝2
①求y关于x的函数关系式
②当x为何值时，△PBC的周长最小，并求出此时y的值。
（1）求证：AB·AF=CB·CD
（2）已知：AB=15cm，BC=9cm，P是射线DE上的动点，设DP=xcm(x>0)，四边形BCDP的面积为y㎝2
①求y关于x的函数关系式
②当x为何值时，△PBC的周长最小，并求出此时y的值。
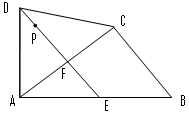
解：（1 ）证△△DCF ∽△ABC
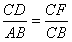即 
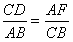
（2）①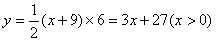
②当P与E重合时，PB+PA最小。x=25, y=
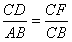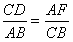
即 （2）①
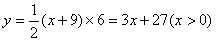
②当P与E重合时，PB+PA最小。x=25, y=
练习册系列答案
阅读快车系列答案
相关题目
如图，四边形ABCD的对角线AC与BD互相垂直平分于点O，设AC=2a，BD=2b，请推导这个四边形的性质．（至少3条）
如图，四边形ABCD的对角线AC、BD交于点P，过点P作直线交AD于点E，交BC于点F．若PE=PF，且AP+AE=CP+CF．
如图，四边形ABCD，AB=AD=2，BC=3，CD=1，∠A=90°，求∠ADC的度数．
如图，四边形ABCD为正方形，E是BC的延长线上的一点，且AC=CE，求∠DAE的度数．