题目内容
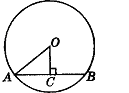
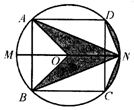
已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O的切线分别交过A、B两点的切线于D、C, AC、BD相交于N点,连结ON、NP,下列结论:①四边形ANPD是梯形; ② ON=NP; ③ DP·PC为定值; ④PA为∠NPD的平分线.其中一定成立的是( )

A. ①②③ B.②③④ C. ①③④ D. ①④

A. ①②③ B.②③④ C. ①③④ D. ①④
C
①因为DA、DP、CP、CB为⊙O切线,故DA⊥AB,CB⊥AB.
于是AD∥BC,AD=DP,CB=CP.
∴∠CAD=∠NCB,∠ADN=∠DBC,
∴△AND∽△CNB,
∴CB/AD=CN/NA=CP/DP,
∴NP∥BC,
故NP∥AD,又AN与DP相交,
∴四边形ANPD是梯形,本选项正确;
②不能确定;
③连接OP,OD,OC,如图所示:

由DA,DP为圆O的切线,
∴∠OAD=∠OPD=90°,
在直角三角形OAD和OPD中,
DA=DP,OD=OD,
∴△OAD≌△OPD,
∴∠AOD=∠POD,
同理∠POC=∠BOC,
∠AOD+∠DOP+∠POC+∠BOC=180°,
∴∠COD=∠DOP+∠COP=90°,又OP⊥CD,
∴∠POD+∠POC=90°,∠POD+∠ODP=90°,
∴∠ODP=∠POC,同理∠POD=∠PCO,
∴△OPD∽△CPO,
∴OP/PC=DP/OP,
即OP2=DP?PC,
∵OP为圆O的半径,为定值,故DP?PC为定值,本选项正确;
④因为DA=DP,所以∠DAP=∠DPA.
因为NP∥AD,所以∠NPA=∠DAP.
所以∠DPA=∠NPA.
PA为∠NPD的平分线.
则一定成立的选项有:①③④.
故答案为:①③④.
于是AD∥BC,AD=DP,CB=CP.
∴∠CAD=∠NCB,∠ADN=∠DBC,
∴△AND∽△CNB,
∴CB/AD=CN/NA=CP/DP,
∴NP∥BC,
故NP∥AD,又AN与DP相交,
∴四边形ANPD是梯形,本选项正确;
②不能确定;
③连接OP,OD,OC,如图所示:

由DA,DP为圆O的切线,
∴∠OAD=∠OPD=90°,
在直角三角形OAD和OPD中,
DA=DP,OD=OD,
∴△OAD≌△OPD,
∴∠AOD=∠POD,
同理∠POC=∠BOC,
∠AOD+∠DOP+∠POC+∠BOC=180°,
∴∠COD=∠DOP+∠COP=90°,又OP⊥CD,
∴∠POD+∠POC=90°,∠POD+∠ODP=90°,
∴∠ODP=∠POC,同理∠POD=∠PCO,
∴△OPD∽△CPO,
∴OP/PC=DP/OP,
即OP2=DP?PC,
∵OP为圆O的半径,为定值,故DP?PC为定值,本选项正确;
④因为DA=DP,所以∠DAP=∠DPA.
因为NP∥AD,所以∠NPA=∠DAP.
所以∠DPA=∠NPA.
PA为∠NPD的平分线.
则一定成立的选项有:①③④.
故答案为:①③④.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
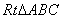 中,
中,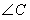 =90°,
=90°,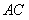 =6,
=6,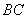 =8.则
=8.则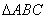 的内切圆半径
的内切圆半径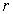 = .
= .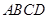 中,
中,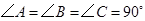 ,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )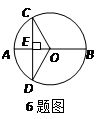
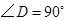
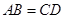
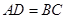
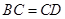
 ,那么∠ACD的度数是( ).
,那么∠ACD的度数是( ).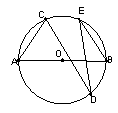
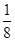
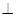 CD于点E. 连接AC、OC、BC。
CD于点E. 连接AC、OC、BC。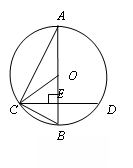
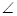 ACO=
ACO=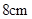 ,CD=
,CD=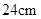 ,求⊙O的直径.
,求⊙O的直径. 