题目内容
用两个全等的含30°角的直角三角形制作如图1所示的两种卡片, 两种卡片中扇形的半径均为1, 且扇形所在圆的圆心分别为长直角边的中点和30°角的顶点, 按先A后B 的顺序交替摆放A、B两种卡片得到图2所示的图案. 若摆放这个图案共用两种卡片8张,则这个图案中阴影部分的面积之和为 ; 若摆放这个图案共用两种卡片(2n+1)张( n为正整数), 则这个图案中阴影部分的面积之和为 . (结果保留p )

 (2分);
(2分);  (2分)
(2分)分别求出A、B两种扇形的面积,再求图形中A、B两种扇形的个数,求阴影部分的面积,注意按先A后B的顺序交替摆放A、B两种卡片.
解答:解:依题意,A种图中扇形圆心角为60°,半径为1,面积为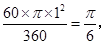
B种图中扇形圆心角为30°,半径为1,面积为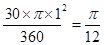 ,
,
故图2中阴影部分面积和为4×( )=π,
)=π,
摆放这个图案共用两种卡片(2n+1)张,需要A种图(n+1)张,需要B种图n张,
则这个图案中阴影部分的面积和为(n+1)×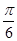 +n×
+n× =
= 故答案为:π,
故答案为:π,
解答:解:依题意,A种图中扇形圆心角为60°,半径为1,面积为
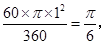
B种图中扇形圆心角为30°,半径为1,面积为
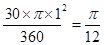 ,
,故图2中阴影部分面积和为4×(
 )=π,
)=π,摆放这个图案共用两种卡片(2n+1)张,需要A种图(n+1)张,需要B种图n张,
则这个图案中阴影部分的面积和为(n+1)×
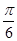 +n×
+n× =
= 故答案为:π,
故答案为:π,

练习册系列答案
相关题目


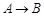 的方向滚动,直至△MNP中有一个点与点B重合为止,则点P经过的路程为__________。
的方向滚动,直至△MNP中有一个点与点B重合为止,则点P经过的路程为__________。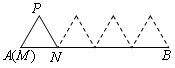
 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦 是小圆的切线,点
是小圆的切线,点 为切点,且
为切点,且 ,
, ,连结
,连结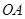 交小圆于点
交小圆于点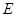 ,则扇形
,则扇形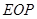 的面积为 .
的面积为 .
 ,求BE的长.
,求BE的长.

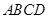 内,作出使
内,作出使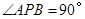 的所有点
的所有点 ,并简要说明作法.
,并简要说明作法. 的所有的点
的所有的点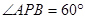 的所有的点
的所有的点