题目内容
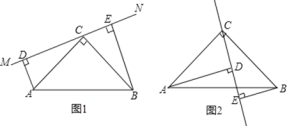
【题目】如图①,在△ABC中,∠BAC=90', AB=AC, AE是过点A的一条直线,且点B, C在AE的异侧,BD⊥AE于点D, CE⊥AE于点E.
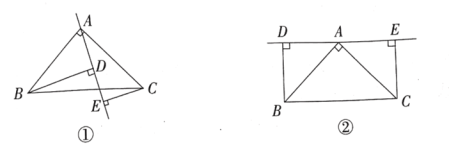
(1)求证: BD=DE +CE ;
(2)若当直线AE旋转到图②位置时,判断BD与DE,CE的数量关系,并说明理由.
【答案】(1)详见解析;(2)BD=DE-CE,理由详见解析.
【解析】
(1)在直角三角形中,由题中条件可得∠ABD=EAC,AB=AC,则可判定Rt△BDA≌Rt△AEC,由三角形全等可得三角形对应边相等,进而通过线段之间的转化,可得出结论;
(2)由题中条件同(1)可证Rt△BDA≌Rt△AEC,得出对应线段相等,进而可得线段之间的关系.
(1)∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠ABD+∠BAD=90°,∠BAD+∠EAC=90,
∴∠ABD=∠EAC,
在Rt△BDA和Rt△AEC中,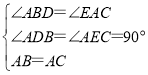 ,
,
∴Rt△BDA≌Rt△AEC(AAS),
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=DE +CE;
(2)BD=DECE,
理由:∵∠BAC=90°,BD⊥AE,CE⊥AE
∴∠ABD+∠BAD=90°,∠BAD+∠EAC=90°,
∴∠ABD=∠EAC,
在Rt△BDA和Rt△AEC中,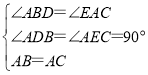 ,
,
∴Rt△BDA≌Rt△AEC(AAS),
∴BD=AE,AD=CE,
∴BD=AE=DEAD=DECE.

练习册系列答案
相关题目