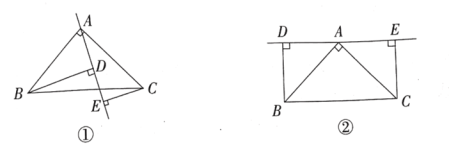��Ŀ����
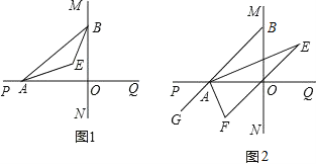
����Ŀ�� ֱ��MN��ֱ��PQ��ֱ�ཻ��O����A������OP���˶�����B������OM���˶���
��1����ͼ1����֪AE��BE�ֱ��ǡ�BAO�͡�ABO�ǵ�ƽ���ߣ���A��B���˶��Ĺ����У���AEB�Ĵ�С�Ƿ�ᷢ���仯���������仯����˵�����ɣ����������仯���������ֵ��
��2����ͼ2���ӳ�BA��G����֪��BAO����OAG�Ľ�ƽ�������BOQ�Ľ�ƽ�������ӳ����ཻ��E��F�����EAF=______��������AEF�У������һ��������һ���ǵ�3���������ABO�Ķ�����
���𰸡���1����AEB�Ĵ�С���䣬Ϊ135�㣻��2��90����ABOΪ60����45����
��������
��1������ֱ��MN��ֱ��PQ��ֱ�ཻ��O��֪��AOB=90��������AE��BE�ֱ��ǡ�BAO�͡�ABO�ǵ�ƽ���ߵó���BAE=![]() ��OAB����ABE=
��OAB����ABE=![]() ��ABO�����������ڽǺͶ������ɵó����ۣ�
��ABO�����������ڽǺͶ������ɵó����ۣ�
��2���ɡ�BAO���BOQ�Ľ�ƽ�����ཻ��E��֪��EAO=![]() ��BAO����EOQ=
��BAO����EOQ=![]() ��BOQ�������ó���E�Ķ�������AE��AF�ֱ��ǡ�BAO�͡�OAG�Ľ�ƽ���߿�֪��EAF=90�����ڡ�AEF�У���һ��������һ���ǵ�3��������������з������ۣ�
��BOQ�������ó���E�Ķ�������AE��AF�ֱ��ǡ�BAO�͡�OAG�Ľ�ƽ���߿�֪��EAF=90�����ڡ�AEF�У���һ��������һ���ǵ�3��������������з������ۣ�
�⣺��1����AEB�Ĵ�С���䣬
��ֱ��MN��ֱ��PQ��ֱ�ཻ��O��
���AOB=90����
���OAB+��OBA=90����
��AE��BE�ֱ��ǡ�BAO�͡�ABO�ǵ�ƽ���ߣ�
���BAE=![]() ��OAB����ABE=
��OAB����ABE=![]() ��ABO��
��ABO��
���BAE+��ABE=![]() (��OAB+��ABO)=
(��OAB+��ABO)=![]() ��90��=45����
��90��=45����
���AEB=135����
��2����AE��AF�ֱ��ǡ�BAO�͡�OAG�Ľ�ƽ���ߣ�
���EAO=![]() ��BAO����FAO=
��BAO����FAO=![]() ��GAO��
��GAO��
���EAF=![]() (��BAO+��GAO)=
(��BAO+��GAO)=![]() ��180��=90����
��180��=90����
�ʴ�Ϊ��90��
�ߡ�BAO���BOQ�Ľ�ƽ�����ཻ��E��
���EAO=![]() ��BAO����EOQ=
��BAO����EOQ=![]() ��BOQ��
��BOQ��
���E=��EOQ-��EAO=![]() (��BOQ-��BAO)=
(��BOQ-��BAO)=![]() ��ABO��
��ABO��
����ABO=2��E��
�ڡ�AEF�У�����һ��������һ���ǵ�3�����ʷ�����������ۣ�
�١�EAF=3��E����E=30�������ABO=60����
�ڡ�EAF=3��F����E=60������ABO=120��(��ȥ)��
�ۡ�F=3��E����E=22.5������ABO=45����
�ܡ�E=3��F����E=67.5������ABO=135��(��ȥ)��
���ABOΪ60����45����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�