题目内容
【题目】为了解青少年形体情况,现随机抽查了若干名初中学生坐姿、站姿、走姿的好坏情况(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:

(1)求这次被抽查形体测评的学生一共有多少人?
(2)求在被调查的学生中三姿良好的学生人数,并将条形统计图补充完整;
(3)若全市有5万名初中生,那么估计全市初中生中,坐姿和站姿不良的学生共有多少人?
【答案】(1)500名;(2)75名;(3)2.5万
【解析】试题分析:(1)用类型人数除以所占百分比就是总人数.(2)用总人数乘以15%.
(3) 坐姿和站姿不良的学生的学生的百分比乘以总人数.
试题解析:
(1)解:100÷20%=500(名),
答:这次被抽查形体测评的学生一共是500名;
(2)解:三姿良好的学生人数:500×15%=75名,
补全统计图如图所示;

(3)解:5万×(20%+30%)=2.5万,
答:全市初中生中,坐姿和站姿不良的学生有2.5万人.
【题型】解答题
【结束】
24
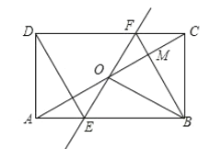
【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.

(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1) 先证明△DOP≌△EOH,再利用等量代换得到PE=DH.
(2) 设DP=x, Rt△BCH中,先用 x表示三角形三边,利用勾股定理列式解方程.
试题解析:
(1)解:证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH,
∴△DOP≌△EOH,
∴OP=OH,
∴PO+OE=OH+OD,
∴PE=DH.
(2)解:设DP=x,则EH=x,BH=10﹣x,
CH=CD﹣DH=CD﹣PE=10﹣(8﹣x)=2+x,
∴在Rt△BCH中,BC2+CH2=BH2
(2+x)2+82=(10﹣x)2,
∴x=![]() ,
,
∴DP=![]() .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案