Question

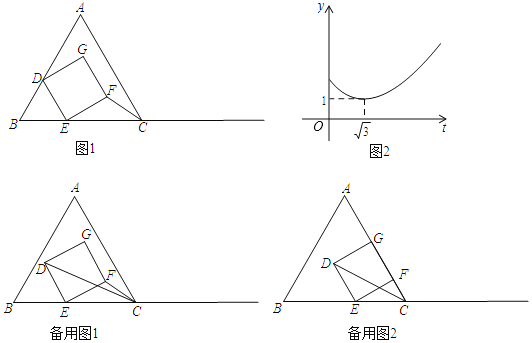
【题目】如图，抛物线y=-x2+4x-1与y轴交于点C，CD∥x轴交抛物线于另一点D，AB∥x轴交抛物线于点A，B，点A在点B的左侧，且两点均在第一象限，BH⊥CD于点H．设点A的横坐标为m．

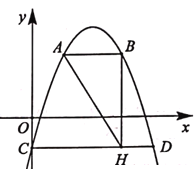
（1）当m=1时，求AB的长.

（2）若AH=（CH-DH），求m的值.

Answer 1

【答案】（1）2；（2）

【解析】

（1）因为A在抛物线上，则把m=1代入二次函数解析式y=-x2+4x-1解得y=2，令-x2+4x-1=2解得的两个根分别是A、B两点的横坐标．由于B点在A点右边，用B点横坐标减去A点横坐标所得的数值就是AB线段的长度．

（2）根据题意以及抛物线的对称性分析可得AB=CH-DH，若AH=（CH-DH），实际上AH=AB，此时△ABH应为等腰直角三角形，∠B为直角，AB=BH，用待定系数法设点A的坐标为（m，-m2+4m-1），再利用等腰三角形边比数量关系设出B点坐标，由于A、B两点关于对称轴直线x=2对称，建立方程求解即可得m的值．

（1）∵m=1，

∴A的横坐标为1，

代入y=-x2+4x-1得，y=2，

∴A（1，2），

把y=2代入y=-x2+4x-1得，2=-x2+4x-1，

解得x1=1，x2=3，

∴B（3，2），

∴AB=3-1=2．

（2）∵AB∥x轴交抛物线于点A，B，

∴A、B两点关于对称轴对称，

∴CH-DH=AB，

∵AH=（CH-DH），

∴AH=AB，

∴，

∴∠BAH=45°，

∴AB=BH，

由A在抛物线上，则设A（m，-m2+4m-1），则B（-m2+5m，-m2+4m-1）．

∴对称轴h=

∴整理得，m2-6m+4=0

解得，m=3+或m=3-

又∵A点在对称轴左边

∴m＜2

∴m=3-