Question

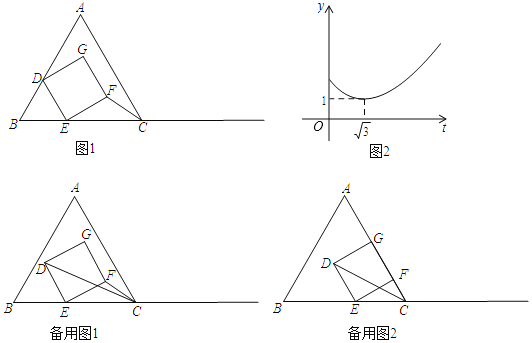
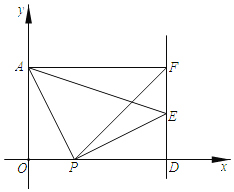
【题目】在平面直角坐标系中，点A坐标为(0，3)，x轴上点P(t，0)，将线段AP绕点P顺时针旋转90°得到PE，过点E作直线l⊥x轴于D，过点A作AF⊥直线l于F．

(1)当点E是DF的中点时，求直线PE的函数表达式．

(2)当t＝5时，求△PEF的面积．

(3)在直线l上是否存在点G，使得∠APO＝∠PFD+∠PGD？若存在，试用t的代数式表示点G的坐标；若不存在，请说明理由．

Answer 1

【答案】(1)y＝；(2)17；(3)G(3+t，﹣).

【解析】

（1）证明Rt△APO≌Rt△PED（HL），得到ED==PO，DO=OP+PD=OP+AO=3+=，求出点E（，），P（，0），将点代入解析式即可求解；

（2）由（1）的全等可得到OD=8，DF=3，所以S△APE=5×8-×3×5×2-×2×8=17；

（3）假设在直线l上是否存在点G，使得∠APO=∠PFD+∠PGD，可以得到A，P，E，F四点共圆，所以∠PAE=∠PFE=45°，PD=FE=3，FP=3，

设E（m，n），由AP⊥PE，，再由等腰直角三角形PDF可得PD=3，D（3+t，0），E（3+t，t）可以证明△APF∽△PGF，所以，即18=（3+t）（3+DG），得到DG=，进而取得G点坐标．

(1)∵线段AP绕点P顺时针旋转90°得到PE，

∴AP＝PE，∠APE＝90°，

∵∠APO+∠PED＝∠APO+∠OAP＝90°，

∴∠PED＝∠APO，

∴Rt△APO≌Rt△PED(HL)，

∴OP＝ED，AO＝PD，

∵OA＝3，点E是DF的中点，

∴ED＝＝PO，

∴DO＝OP+PD＝OP+AO＝3+＝，

∴E(，)，P(，0)

设直线PE的解析式为y＝kx+b，

∴，

∴，

∴y＝；

(2)∵Rt△APO≌Rt△PED，

∴OP＝ED，AO＝PD，

∵OA＝5，OP＝3，

∴OD＝8，DF＝3，

∴S△APE＝5×8﹣×3×5×2﹣×8＝17；

(3)假设在直线l上是否存在点G，使得∠APO＝∠PFD+∠PGD，

∵AP⊥PE，AF⊥FE，

∴A，P，E，F四点共圆，

∴∠PAE＝∠PFE＝45°，

∴∠APF＝∠PGD，

∴PD＝FE＝3，

∴FP＝3，

设E(m，n)，

∵AP⊥PE，

∴，

∵PD＝3，

∴D(3+t，0)，

∴m＝3+t，

∴n＝t，

∴E(3+t，t)

∴△APF∽△PGF，

∴，

∴18＝(3+t)(3+DG)，

∴DG＝，

∴G(3+t，﹣)；