题目内容
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥BD,AC平分∠BAD.
(1)给出下列四个条件:①AB=AD,②OB=OD,③∠ACB=∠ACD,④AD∥BC,上述四个条件中,选择一个合适的条件,使四边形ABCD是菱形,这个条件是(填写序号);
(2)根据所选择的条件,证明四边形ABCD是菱形.
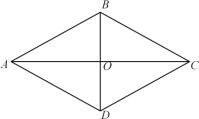
【答案】(1)④(2)见解析
【解析】
(1)根据平行四边形的判定选择的条件能使四边形ABCD是平行四边形,然后即可证明四边形ABCD是菱形;
(2)首先证明△AOB≌△AOD,然后结合AD∥BC可得到AB=AD= BC,根据平行四边形的判定可得四边形ABCD是平行四边形,再由AC⊥BD可证□ABCD是菱形.
解:(1)选择④可以使四边形ABCD是菱形.
(2)证明:
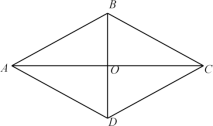
∵AC⊥BD,∴∠AOB=∠AOD=90°.
∵AC平分∠BAD,∴∠BAO=∠DAO.
又∵AO=AO,∴△AOB≌△AOD.
∴AB=AD.
∵AD∥BC,∴∠DAO=∠BCO.
又∵∠BAO=∠DAO,∴∠BAO=∠BCO.
∴BA=BC.
∴AD=BC.
又∵AD∥BC,∴四边形ABCD是平行四边形.
又∵AC⊥BD,∴□ABCD是菱形.

练习册系列答案
相关题目