题目内容
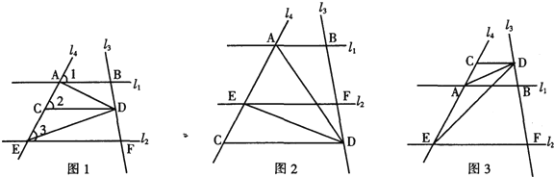
【题目】直线l1平行于直线l2,直线l3、l4分别与l1、l2交于点B、F和A、E,点D是直线l3上一动点,DC∥AB交l4于点C.
(1)如图,当点D在l1、l2两线之间运动时,试找出∠BAD、∠DEF、∠ADE之间的关系,并说明理由;

(2)当点D在l1、l2两线外侧运动时,试探究∠BAD、∠DEF、∠ADE之间的关系(点D和B、F不重合),画出图形,给出结论,不必说明理由.
【答案】(1) ∠BAD+DEF=∠ADE;(2) ①当点D在BF的延长线上运动时(如图2),∠BAD=∠ADE+∠DEF;②当点D在FB的延长线上运动时(如图3),∠DEF=∠ADE+∠BAD.
【解析】
(1)由AB∥CD,根据平行线的性质得到∠BAD=∠ADC,而l1∥l2,则CD∥EF,得到∠DEF=∠CDE,于是∠BAD+DEF=∠ADE;
(2)讨论:当点D在BF的延长线上运动时(如图2),由(1)得到∠BAD=∠ADC,∠DEF=∠CDE,则∠BAD=∠ADE+∠DEF;当点D在FB的延长线上运动时(如图3),∠DEF=∠ADE+∠BAD.
(1)∠BAD+∠DEF=∠ADE
理由如下:(如图1)
∵AB∥CD,
∴∠BAD=∠ADC(两直线平行,内错角相等),
∵l1∥l2,
∴CD∥EF,
∴∠DEF=∠CDE(两直线平行,内错角相等),
故∠BAD+∠DEF=∠ADC+∠CDE.
即∠BAD+DEF=∠ADE;
(2)有两种情况:
①当点D在BF的延长线上运动时(如图2),∠BAD=∠ADE+∠DEF;
②当点D在FB的延长线上运动时(如图3),∠DEF=∠ADE+∠BAD.

【题目】某村庄计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积和可供使用农户数见下表:
型号 | 占地面积 (单位:m2/个) | 可供使用农户数 (单位:户/个) |
A | 15 | 18 |
B | 20 | 30 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)如何合理分配建造A,B型号“沼气池”的个数才能满足条件?满足条件的方案有几种?通过计算分别写出各种方案.
(2)请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式;
(3)若A型号“沼气池”每个造价2万元,B型号“沼气池”每个造价3万元,试说明在(1)中的各种建造方案中,哪种建造方案最省钱,最少的费用需要多少万元?