题目内容
【题目】已知关于
、
的方程组
.
（1）求方程组的解（用含
的代数式表示）；
（2）若方程组的解满足为非正数，为负数，求的取值范围：
（3）在（2）的条件下，当为何整数时，不等式
的解集为
?
【答案】（1）
；（2）-2＜m≤2；（3）当m为整数-1或0时，不等式（m-1）x＜m-1的解集为x＞1．
【解析】
（1）利用加减法解关于x、y的方程组；
（2）利用方程组的解得到
，然后解关于m的不等式组；
（3）利用不等式性质得到m-1＜0，即m＜1，加上（2）的结论得到-2＜m＜1，然后写出此范围内的整数即可．
解：（1）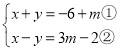
由①+②，得2x=4m-8，解得x=2m-4，
由①-②，得2y=-2m-4，解得y=-m-2，
所以原方程组的解是；
（2）∵x为非正数，y为负数，
∴x≤0，y＜0，
即，
解这个不等式组得-2＜m≤2；
（3）∵不等式（m-1）x＜m-1的解集为x＞1，
∴m-1＜0，即m＜1，
∵-2＜m≤2，
∴-2＜m＜1，
∴整数m为-1，0，
即当m为整数-1或0时，不等式（m-1）x＜m-1的解集为x＞1．
【题目】某村庄计划建造A，B两种型号的沼气池共20个，以解决该村所有农户的燃料问题．两种型号沼气池的占地面积和可供使用农户数见下表：
型号 | 占地面积 （单位：m2/个） | 可供使用农户数 （单位：户/个） |
A | 15 | 18 |
B | 20 | 30 |
已知可供建造沼气池的占地面积不超过365m2，该村农户共有492户．
（1）如何合理分配建造A，B型号“沼气池”的个数才能满足条件？满足条件的方案有几种？通过计算分别写出各种方案．
（2）请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式；
（3）若A型号“沼气池”每个造价2万元，B型号“沼气池”每个造价3万元，试说明在（1）中的各种建造方案中，哪种建造方案最省钱，最少的费用需要多少万元？
