题目内容
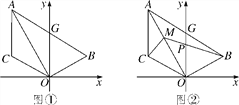
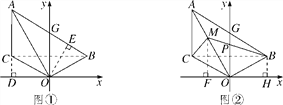
【题目】如图①,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴于G,连接OB,OC.
(1)判断△AOG的形状,并予以证明;
(2)若点B,C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图②,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标.
【答案】(1)△AOG是等腰三角形;(2)见解析;(3)M(-1,3).
【解析】
(1)、利用已知条件可证明∠GOA=∠GAO,由等腰三角形的判定可得AG=OG,所以△AOG是等腰三角形;(2)、由已知可得BP=CP,因为AC∥y轴,可得GA=GB;根据等腰三角形的性质得出∠GOB=∠GBO,∠AOG=∠OAG,所以∠AOG+∠BOG=∠OAG+∠OBG,即∠AOB=∠OAG+∠OBG,即可求得∠AOB=90°;(2)、先证得BM是∠ABC的平分线,设∠OBC=x,则x+∠POB=90°,而∠POA+∠POB=∠AOB=90°,求得x=∠POA,进一步证得x=∠GAM.根据∠OMB=∠GAM+∠ABM=x+∠ABM=x+∠PBM=∠MBO,得出OB=OM,然后证明出△OMF和△BOH全等,根据点B的坐标得出点M的坐标.
(1)解:△AOG的形状是等腰三角形
证明如下:∵AC∥y轴,∴∠CAO=∠GOA, ∵AO平分∠BAC,∴∠CAO=∠GAO,
∴∠GOA=∠GAO,∴AG=OG,∴△AOG是等腰三角形.
(2)证明:如图①,连接BC,过点O作OE⊥AB于点E,过点C作CD⊥x轴于点D.
∵B,C关于y轴对称,AC∥y轴,∴OB=OC,AC⊥BC,∴点A,C,D在同一条直线上.
∵AO为∠CAB的平分线,∴OD=OE.
在Rt△COD和Rt△BOE中,OD=OE,OC=OB,∴△COD≌△BOE(HL),∴∠DCO=∠EBO.
∵∠DCO+∠ACO=180°,∴在四边形ACOB中,∠ACO+∠EBO=180°,
∴∠BAC+∠BOC=180°, 设∠BAO=∠CAO=x,∠OBC=∠OCB=y,
∴2x+∠BOC=180°,2y+∠BOC=180°,∴x=y, ∴∠OAC=∠OBC,
∴∠AOB=∠ACB=90°,∴AO⊥OB.
(3)解:如图②,连接BC,过点M作MF⊥x轴于F,过点B作BH⊥x轴于H,
由(2)可知∠ACB=90°, ∵∠ACM=45°,∴CM平分∠ACB,
又∵AM平分∠BAC,∴BM平分∠ABC.设∠ABM=∠CBM=z,
由(2)可得∠OMB=x+z,∠OBM=y+z=x+z,∴∠OMB=∠OBM,∴OM=OB,
∴△OBM为等腰直角三角形. ∵∠BOH+∠MOF=90°,∠MOF+∠FMO=90°,
∴∠FMO=∠BOH,
在△OMF和△BOH中,∠MFO=∠OHB=90°,∠FMO=∠HOB,OM=OB,∴△OMF≌△BOH(AAS).
又∵点B的坐标为(3,1),∴OF=BH=1,MF=OH=3,∴M(-1,3).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案