题目内容
【题目】如图1，已知数轴上有三点A、B、C，AB＝60，点A对应的数是40．
（1）若
，求点C到原点的距离；
（2）如图2，在（1）的条件下，动点P、Q两点同时从C、A出发向右运动，同时动点R从点A向左运动，已知点P的速度是点R的速度的3倍，点Q的速度是点R的速度2倍少5个单位长度/秒．经过5秒，点P、Q之间的距离与点Q、R之间的距离相等，求动点Q的速度；
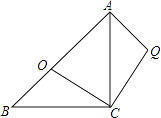
（3）如图3，在（1）的条件下，O表示原点，动点P、T分别从C、O两点同时出发向左运动，同时动点R从点A出发向右运动，点P、T、R的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒，在运动过程中，如果点M为线段PT的中点，点N为线段OR的中点．请问
的值是否会发生变化？若不变，请求出相应的数值；若变化，请说明理由．
【答案】（1）100；（2）7个单位长度/秒；（3）不会发生改变，定值为30．
【解析】
试题分析：（1）首先根据比值得出AC的长度，然后根据数轴的性质得出点C所表示的数，从而得到距离；（2）设R的速度为每秒x个单位，从而分别得出R、P、Q所对应的数，求出PQ和QR的长度，然后根据题意列出方程得出答案；（3）首先设运动时间为t秒，求出点P、T、R、M、N所对应的数，求出PT和MN的长度，然后得出PT－MN的值．
试题解析：（1）根据题意可得：AC=140，则点C所表示的数为40－140=－100
∴点C到原点的距离为100；
（2）设R的速度为每秒x个单位，则R对应的数为
，P对应的数为
， Q对应的数为
，
PQ＝
或
QR＝
∵PQ＝QR ∴
或
解得x＝－9（不合题意，故舍去）或x＝7 ∴动点Q的速度是7个单位长度/秒．
（3）设运动时间为t秒，P对应的数为
，T对应的数为
，R对应的数为
， PT＝
M对应的数为
，N对应的数为
， MN＝
∴PT－MN＝30
∴
的值不会发生变化，是30．
