题目内容
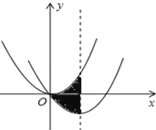
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为
x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为![]() ,则a、b的值分别为( )
,则a、b的值分别为( )
A. ![]() ,
,![]() B.
B. ![]() ,﹣
,﹣![]() C.
C. ![]() ,﹣
,﹣![]() D. ﹣
D. ﹣![]() ,
,![]()
【答案】C
【解析】
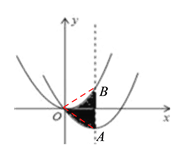
如下图,设平移后所得新抛物线的对称轴和两抛物线相交于点A和点B,连接OA,OB,则由抛物线平移的性质可知,a=![]() ,S阴影=S△OAB,由
,S阴影=S△OAB,由![]() ,可得点A的坐标为
,可得点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,由此可得S△OAB=
,由此可得S△OAB=![]() ,从而可解得b=
,从而可解得b=![]() .
.
如下图,设平移后所得新抛物线的对称轴和两抛物线相交于点A和点B,连接OA,OB,则由抛物线平移的性质可知,a=![]() ,S阴影=S△OAB,
,S阴影=S△OAB,
∴![]() ,
,
∴点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,
,
∴AB=![]() ,点O到AB的距离:
,点O到AB的距离:![]() ,
,
∴S△AOB=![]() ,解得:
,解得:![]() .
.
综上所述,![]() .
.
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目