题目内容
【题目】如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).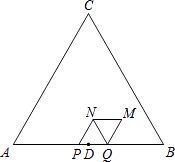
(1)当点N落在边BC上时,求t的值.
(2)当点N到点A、B的距离相等时,求t的值.
(3)当点Q沿D→B运动时,求S与t之间的函数表达式.
(4)设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF与四边形PQMN的面积比为2:3时t的值.
【答案】
(1)
解:∵△PQN与△ABC都是等边三角形,
∴当点N落在边BC上时,点Q与点B重合.
∴DQ=3
∴2t=3.
∴t= ![]()
(2)
解:∵当点N到点A、B的距离相等时,点N在边AB的中线上,
∴PD=DQ,
当0<t< ![]() 时,
时,
此时,PD=t,DQ=2t
∴t=2t
∴t=0(不合题意,舍去),
当 ![]() ≤t<3时,
≤t<3时,
此时,PD=t,DQ=6﹣2t
∴t=6﹣2t,
解得t=2;
综上所述,当点N到点A、B的距离相等时,t=2
(3)
解:由题意知:此时,PD=t,DQ=2t
当点M在BC边上时,
∴MN=BQ
∵PQ=MN=3t,BQ=3﹣2t
∴3t=3﹣2t
∴解得t= ![]()
如图①,当 ![]() 时,
时,
S△PNQ= ![]() PQ2=
PQ2= ![]() t2;
t2;
∴S=S菱形PQMN=2S△PNQ= ![]() t2,
t2,
如图②,当 ![]() 时,
时,
设MN、MQ与边BC的交点分别是E、F,
∵MN=PQ=3t,NE=BQ=3﹣2t,
∴ME=MN﹣NE=PQ﹣BQ=5t﹣3,
∵△EMF是等边三角形,
∴S△EMF= ![]() ME2=
ME2= ![]() (5t﹣3)2
(5t﹣3)2
![]() .
. ![]()
(4)
解:MN、MQ与边BC的交点分别是E、F,
此时, ![]() <t<
<t< ![]() ,
,
t=1或 ![]() .
.
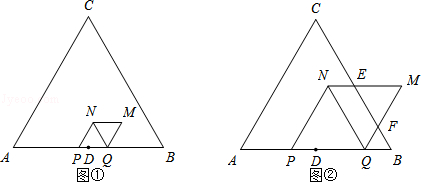
【解析】(1)由题意知:当点N落在边BC上时,点Q与点B重合,此时DQ=3;(2)当点N到点A、B的距离相等时,点N在边AB的中线上,此时PD=DQ;(3)当 ![]() 时,四边形PQMN与△ABC重叠部分图形为四边形PQMN;当
时,四边形PQMN与△ABC重叠部分图形为四边形PQMN;当 ![]() 时,四边形PQMN与△ABC重叠部分图形为五边形PQFEN.(4)MN、MQ与边BC的有交点时,此时
时,四边形PQMN与△ABC重叠部分图形为五边形PQFEN.(4)MN、MQ与边BC的有交点时,此时 ![]() <t<
<t< ![]() ,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.
,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.
【考点精析】关于本题考查的相似三角形的应用,需要了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能得出正确答案.

【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
【题目】如图,在Rt△ABC中,∠B=90°,按如下步骤作图: ①分别以点B、C为圆心,大于 ![]() AB的长为半径作弧,两弧相交于点M和N;
AB的长为半径作弧,两弧相交于点M和N;
②作直线MN交AC于点D,
③连接BD,
若AC=8,则BD的长为 . 
【题目】为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校的人数多于乙校的人数,且甲校的人数不足90人)准备统一购买服装参加演出;下面是某服装厂给出的演出服装的价格表
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
(1)如果两所学校分别单独购买服装一共应付5000元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.